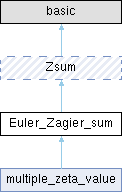
A Euler-Zagier sum is a special case of a Zsum. More...
#include <Euler_Zagier_sum.h>
Public Member Functions | |
| Euler_Zagier_sum (const GiNaC::ex &nc) | |
| Euler_Zagier_sum (const GiNaC::ex &nc, const GiNaC::ex &llc) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| GiNaC::return_type_t | return_type_tinfo () const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | convert_to_Ssum_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1) const override |
| GiNaC::ex | shuffle_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1, const GiNaC::exvector &Z2) const override |
| GiNaC::ex | set_index (const GiNaC::ex &i) const override |
| GiNaC::ex | shift_plus_one (void) const override |
| GiNaC::ex | shift_minus_one (void) const override |
| GiNaC::ex | adjust_upper_limit_downwards (const GiNaC::ex &i) const override |
| GiNaC::ex | adjust_upper_limit_upwards (const GiNaC::ex &i) const override |
| GiNaC::ex | adjust_upper_limit_plus_one (void) const override |
| GiNaC::ex | remove_first_letter (void) const override |
| GiNaC::ex | remove_first_letter (const GiNaC::ex &nc) const override |
 Public Member Functions inherited from Zsum Public Member Functions inherited from Zsum | |
| Zsum (const GiNaC::ex &nc) | |
| Zsum (const GiNaC::ex &nc, const GiNaC::ex &llc) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | index_eq_one (void) const |
| virtual GiNaC::ex | get_head (int k) const |
| virtual GiNaC::ex | get_tail (int k) const |
| virtual GiNaC::ex | antipode (void) const |
| virtual GiNaC::ex | expand_members (int level=0) const |
| virtual GiNaC::ex | eval_explicit () const |
| virtual GiNaC::ex | get_first_letter (void) const |
| virtual GiNaC::ex | prepend_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | prepend_letter (const GiNaC::ex &nc, const GiNaC::ex &lc) const |
| virtual GiNaC::ex | append_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | append_letter_list (const GiNaC::ex &lc) const |
| GiNaC::ex | get_index (void) const |
| GiNaC::ex | get_letter_list (void) const |
| unsigned | get_depth (void) const |
| GiNaC::ex | get_weight (void) const |
Additional Inherited Members | |
 Protected Member Functions inherited from Zsum Protected Member Functions inherited from Zsum | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
| virtual GiNaC::ex | cast_to_Ssum (void) const |
| virtual GiNaC::ex | multiply_letter_with_last_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | multiply_letter_with_first_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | concat_two_sums (const GiNaC::ex &Z1, const GiNaC::ex &Z2) const |
 Protected Attributes inherited from Zsum Protected Attributes inherited from Zsum | |
| GiNaC::ex | n |
| GiNaC::ex | letter_list |
Detailed Description
A Euler-Zagier sum is a special case of a Zsum.
Euler-Zagier sums are recursively defined by
![\[
Z_{m_1,...,m_k}(n) = \sum\limits_{i=1}^n \frac{1}{i^{m_1}} Z_{m_2,...,m_k}(i-1)
\]](form_65.png)
with
![\[
Z(n) = 1
\]](form_66.png)
for 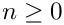
Member Function Documentation
◆ adjust_upper_limit_downwards()
|
overridevirtual |
Adjusts the upper summation limit 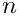
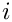
![\[
Z(n;m_1,...;1,...) = Z(i;m_1,...;1,...)
+ \sum\limits_{j=1}^{n-i} \frac{1}{(i+j)^{m_1}} Z(i-1+j;m_2,...;1,...)
\]](form_55.png)
with 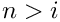
For the empty sum we have
![\[
Z(n) = Z(i)
\]](form_57.png)
This routine assumes 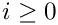
Reimplemented from Zsum.
◆ adjust_upper_limit_plus_one()
|
overridevirtual |
◆ adjust_upper_limit_upwards()
|
overridevirtual |
Adjusts the upper summation limit 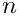
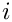
![\[
Z(n;m_1,...;1,...) = Z(i;m_1,...;1,...)
\mbox{} - \sum\limits_{j=0}^{i-n-1} \frac{1}{(i-j)^{m_1}} Z(i-j-1;m_2,...;1,...)
\]](form_59.png)
with 
For the empty sum we have
![\[
Z(n) = Z(i)
\]](form_57.png)
This routine assumes 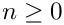
This routine might give rise to poles for some values of 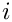
Reimplemented from Zsum.
◆ convert_to_Ssum_exvector()
|
overridevirtual |
A more efficient version for the conversion to harmonic sums, based on exvector (e.g. std::vector<GiNaC::ex> ). Z0 contains the result. Z1 is reversed order, so that we can use pop_back.
Reimplemented from Zsum.
◆ eval()
|
override |
The simplifications are done in the following order:
- If the upper summation limit is equal to infinity, we have a multiple zeta value.
- If the upper summation index is an integer, perform the sum explicitly.
◆ remove_first_letter() [1/2]
|
overridevirtual |
Reimplemented from Zsum.
◆ remove_first_letter() [2/2]
|
overridevirtual |
Returns a Euler_Zagier_sum with the first letter removed from the letter_list.
Reimplemented from Zsum.
◆ set_index()
|
overridevirtual |
Sets the upper summation index to 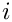
Reimplemented from Zsum.
◆ shift_minus_one()
|
overridevirtual |
Returns 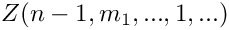
Reimplemented from Zsum.
◆ shift_plus_one()
|
overridevirtual |
Returns 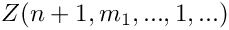
Reimplemented from Zsum.
◆ shuffle_exvector()
|
overridevirtual |
A more efficient version for the multiplication of Euler_Zagier_sums, based on exvector (e.g. std::vector<GiNaC::ex> ). Z0 contains the result. Z1 and Z2 are in reversed order, so that we can use pop_back.
Reimplemented from Zsum.
The documentation for this class was generated from the following files:
Generated by
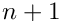
![\[
Z(n;m_1,...;1,...) = Z(n+1;m_1,...;1,...)
\mbox{} - \frac{1}{(n+1)^{m_1}} Z(n;m_2,...;1,...).
\]](form_63.png)