Classes | |
| class | basic_letter |
| A basic_letter is an element of an alphabet. More... | |
| class | Bsum |
| Bsums arise from Hoelder convolutions. More... | |
| class | classical_polylog |
| A classical polylog is a special case of a Nielsen polylog. More... | |
| class | Csum |
| Csums involve a conjugation. More... | |
| class | Euler_Zagier_sum |
| A Euler-Zagier sum is a special case of a Zsum. More... | |
| class | expand_request |
| Flags for the nestedsum_helper_expand function. More... | |
| class | expand_status |
| Flags for the status of the expansion. More... | |
| class | harmonic_polylog |
| A harmonic polylog is a special case of a multiple polylog. More... | |
| class | harmonic_sum |
| A harmonic sum is a special case of a Ssum. More... | |
| class | harmonic_sum_to_Infinity |
| class | hash_entry |
| This class provides a container for expressions to be stored in hash tables. More... | |
| class | letter |
| A letter is a basic_letter with offset=0. More... | |
| class | list_of_tgamma |
| The class list_of_tgamma is a container for the class ratio_of_tgamma. More... | |
| struct | map_insert_Zsums |
| struct | map_remove_Zsums |
| class | multiple_polylog |
| A multiple polylog sum is a special case of a Zsum. More... | |
| class | multiple_zeta_value |
| class | nestedsums_helper_less |
| class | nestedsums_status_flags |
| Additional status flags. More... | |
| class | nielsen_polylog |
| A Nielsen polylog is a special case of a harmonic polylog. More... | |
| class | print_format |
| Flags for the print format for polylogs. More... | |
| class | ratio_of_tgamma |
| The class ratio_of_tgamma contains the ratio of two Gamma functions. More... | |
| class | root_of_unity |
| class | Ssum |
| Ssums form an algebra. More... | |
| class | Ssum_to_Infinity |
| A Ssum_to_Infinity is a special case of a Ssum. More... | |
| class | transcendental_fct_type_A |
| class | transcendental_fct_type_B |
| class | transcendental_fct_type_C |
| class | transcendental_fct_type_D |
| class | transcendental_sum_type_A |
| class | transcendental_sum_type_B |
| The class transcendental_sum_type_B may contain | |
| class | transcendental_sum_type_C |
| The class transcendental_sum_type_C involves a conjugation. More... | |
| class | transcendental_sum_type_D |
| class | unit_letter |
| A unit_letter is a letter whose letter content equals 1. More... | |
| class | Zsum |
| Zsums form a Hopf algebra. More... | |
Typedefs | |
| typedef unsigned int | p_int |
Functions | |
| GINAC_BIND_UNARCHIVER (basic_letter) | |
| GiNaC::ex | concat (const basic_letter &l1, const basic_letter &l2) |
| GINAC_DECLARE_UNARCHIVER (basic_letter) | |
| GiNaC::ex | create_basic_letter (const GiNaC::ex &l, const GiNaC::ex &d, const GiNaC::ex &o) |
| GiNaC::ex | create_basic_letter (const GiNaC::ex &l, const GiNaC::ex &d, const GiNaC::ex &o, const GiNaC::ex &i) |
| GINAC_BIND_UNARCHIVER (Bsum) | |
| ex | convert_Bsum_to_Ssum (const ex &C) |
| ex | convert_Bsum_to_Zsum (const ex &C) |
| ex | create_Bsum_from_exvector (const ex &nc, const exvector &v) |
| GINAC_DECLARE_UNARCHIVER (Bsum) | |
| GiNaC::ex | create_Bsum (const GiNaC::ex &nc, const GiNaC::ex &llc) |
| GiNaC::ex | create_Bsum_from_exvector (const GiNaC::ex &nc, const GiNaC::exvector &v) |
| GiNaC::ex | convert_Bsum_to_Ssum (const GiNaC::ex &C) |
| GiNaC::ex | convert_Bsum_to_Zsum (const GiNaC::ex &C) |
| GINAC_BIND_UNARCHIVER (classical_polylog) | |
| GINAC_DECLARE_UNARCHIVER (classical_polylog) | |
| GiNaC::ex | create_classical_polylog (const GiNaC::ex &llc) |
| const symbol | Infinity ("Infinity","\\infty") |
| const symbol | _default ("default") |
| const symbol | _default_index ("dummy") |
| GINAC_BIND_UNARCHIVER (Csum) | |
| ex | convert_Csum_to_Ssum (const ex &C) |
| ex | convert_Csum_to_Zsum (const ex &C) |
| ex | create_Csum_from_exvector (const ex &nc, const exvector &v) |
| GINAC_DECLARE_UNARCHIVER (Csum) | |
| GiNaC::ex | create_Csum (const GiNaC::ex &nc, const GiNaC::ex &llc) |
| GiNaC::ex | create_Csum_from_exvector (const GiNaC::ex &nc, const GiNaC::exvector &v) |
| GiNaC::ex | convert_Csum_to_Ssum (const GiNaC::ex &C) |
| GiNaC::ex | convert_Csum_to_Zsum (const GiNaC::ex &C) |
| GINAC_BIND_UNARCHIVER (Euler_Zagier_sum) | |
| ex | create_Euler_Zagier_sum_with_ones (const ex &n, const int &k) |
| ex | create_Euler_Zagier_sum_from_exvector (const ex &nc, const exvector &v) |
| GINAC_DECLARE_UNARCHIVER (Euler_Zagier_sum) | |
| GiNaC::ex | create_Euler_Zagier_sum (const GiNaC::ex &nc, const GiNaC::ex &llc) |
| GiNaC::ex | create_Euler_Zagier_sum_with_ones (const GiNaC::ex &n, const int &k) |
| GiNaC::ex | create_Euler_Zagier_sum_from_exvector (const GiNaC::ex &nc, const GiNaC::exvector &v) |
| static ex | Harmonic_sum_eval (const ex &x1, const ex &x2) |
| REGISTER_FUNCTION (Harmonic_sum, eval_func(Harmonic_sum_eval)) | |
| static ex | EulerZagier_sum_eval (const ex &x1, const ex &x2) |
| REGISTER_FUNCTION (EulerZagier_sum, eval_func(EulerZagier_sum_eval)) | |
| static ex | S_sum_infinity_eval (const ex &x1, const ex &x2) |
| REGISTER_FUNCTION (S_sum_infinity, eval_func(S_sum_infinity_eval)) | |
| static ex | S_sum_eval (const ex &x1, const ex &x2, const ex &x3) |
| REGISTER_FUNCTION (S_sum, eval_func(S_sum_eval)) | |
| static ex | Z_sum_eval (const ex &x1, const ex &x2, const ex &x3) |
| REGISTER_FUNCTION (Z_sum, eval_func(Z_sum_eval)) | |
| ex | convert_to_nestedsums (const ex &e) |
| ex | convert_to_ginac_functions (const ex &e) |
| GiNaC::ex | convert_to_nestedsums (const GiNaC::ex &e) |
| GiNaC::ex | convert_to_ginac_functions (const GiNaC::ex &e) |
| GINAC_BIND_UNARCHIVER (harmonic_polylog) | |
| GINAC_DECLARE_UNARCHIVER (harmonic_polylog) | |
| GiNaC::ex | create_harmonic_polylog (const GiNaC::ex &llc) |
| GINAC_BIND_UNARCHIVER (harmonic_sum) | |
| ex | create_harmonic_sum_with_ones (const ex &n, const int &k) |
| ex | create_harmonic_sum_from_exvector (const ex &nc, const exvector &v) |
| GINAC_DECLARE_UNARCHIVER (harmonic_sum) | |
| GiNaC::ex | create_harmonic_sum (const GiNaC::ex &nc, const GiNaC::ex &llc) |
| GiNaC::ex | create_harmonic_sum_with_ones (const GiNaC::ex &n, const int &k) |
| GiNaC::ex | create_harmonic_sum_from_exvector (const GiNaC::ex &nc, const GiNaC::exvector &v) |
| GINAC_BIND_UNARCHIVER (harmonic_sum_to_Infinity) | |
| GINAC_DECLARE_UNARCHIVER (harmonic_sum_to_Infinity) | |
| GiNaC::ex | create_harmonic_sum_to_Infinity (const GiNaC::ex &llc) |
| GINAC_BIND_UNARCHIVER (hash_entry) | |
| GINAC_DECLARE_UNARCHIVER (hash_entry) | |
| GiNaC::ex | create_hash_entry (const GiNaC::ex &cd, const GiNaC::ex &sd, const GiNaC::ex &rd, unsigned rkey) |
| ex | nestedsums_helper_eval (const ex &expr) |
| ex | nestedsums_helper_expand (const ex &expr, int level) |
| ex | nestedsums_helper_multiply_via_triangle (const ex &A, const ex &B, const ex &expansion_parameter, int order) |
| ex | nestedsums_helper_multiply_via_triangle_speedy (const ex &A, const ex &B, const ex &expansion_parameter, int order) |
| ex | nestedsums_helper_multiply_laurent (const ex &A, const ex &B, const ex &expansion_parameter, int order) |
| ex | nestedsums_helper_multiply_laurent_speedy (const ex &A, const ex &B, const ex &expansion_parameter, int order) |
| ex | nestedsums_helper_expand_tgamma_fct (const ex &a1, const ex &b1, const ex &a2, const ex &b2, const ex &expansion_parameter, int order) |
| ex | nestedsums_helper_expand_lst_tgamma_fct (const ex &ll1, const ex &ll2, const ex &expansion_parameter, int order) |
| ex | nestedsums_helper_series (const ex &f, const ex &expansion_parameter, int order) |
| exvector | exvector_from_lst (const ex &l) |
| exvector | reverse_exvector_from_lst (const ex &l) |
| exvector | exvector_append_lst (const exvector &v, const ex &l) |
| exvector | exvector_multiply_last_letter (const exvector &v, const ex &x) |
| exvector | exvector_increase_last_degree (const exvector &v) |
| ex | nestedsums_helper_bernoulli (int n) |
| ex | nestedsums_helper_lowering_op_geo_0 (const ex &x, int m) |
| ex | nestedsums_helper_lowering_op_geo_1 (const ex &x, int m) |
| ex | nestedsums_helper_arithmetic_sum_type_Z (const ex &n, const ex &m) |
| ex | nestedsums_helper_arithmetic_sum_type_S (const ex &n, const ex &m) |
| ex | nestedsums_helper_expand_power (const ex &x, const ex &m, const ex &expansion_parameter, int order) |
| int | nestedsums_helper_get_degree (const ex &expr, const ex &eps) |
| int | nestedsums_helper_ldegree (const ex &expr, const ex &eps) |
| ex | nestedsums_helper_coeff (const ex &expr, const ex &eps, int n) |
| bool | is_class_in_nestedsums (const ex &expr) |
| bool | is_expr_in_sym_lst (const ex &expr, const lst &sym_lst) |
| ex | nestedsums_helper_normalize (const ex &expr, const lst &sym_lst) |
| ex | nestedsums_helper_sort (const ex &expr, const lst &sym_lst) |
| ex | convert_Zsums_to_standard_form (const ex &expr, const lst &sym_lst) |
| void | nestedsums_helper_clear_hashes (void) |
| GiNaC::ex | nestedsums_helper_eval (const GiNaC::ex &expr) |
| GiNaC::ex | nestedsums_helper_expand (const GiNaC::ex &expr, int level=0) |
| GiNaC::ex | nestedsums_helper_multiply_via_triangle (const GiNaC::ex &A, const GiNaC::ex &B, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_multiply_via_triangle_speedy (const GiNaC::ex &A, const GiNaC::ex &B, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_multiply_laurent (const GiNaC::ex &A, const GiNaC::ex &B, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_multiply_laurent_speedy (const GiNaC::ex &A, const GiNaC::ex &B, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_expand_tgamma_fct (const GiNaC::ex &a1, const GiNaC::ex &b1, const GiNaC::ex &a2, const GiNaC::ex &b2, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_expand_lst_tgamma_fct (const GiNaC::ex &ll1, const GiNaC::ex &ll2, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_expand_power (const GiNaC::ex &x, const GiNaC::ex &m, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_series (const GiNaC::ex &f, const GiNaC::ex &expansion_parameter, int order) |
| GiNaC::ex | nestedsums_helper_lowering_op_geo_0 (const GiNaC::ex &x, int m) |
| GiNaC::ex | nestedsums_helper_lowering_op_geo_1 (const GiNaC::ex &x, int m) |
| GiNaC::ex | nestedsums_helper_arithmetic_sum_type_Z (const GiNaC::ex &n, const GiNaC::ex &m) |
| GiNaC::ex | nestedsums_helper_arithmetic_sum_type_S (const GiNaC::ex &n, const GiNaC::ex &m) |
| int | nestedsums_helper_get_degree (const GiNaC::ex &expr, const GiNaC::ex &eps) |
| int | nestedsums_helper_ldegree (const GiNaC::ex &expr, const GiNaC::ex &eps) |
| GiNaC::ex | nestedsums_helper_coeff (const GiNaC::ex &expr, const GiNaC::ex &eps, int n=1) |
| GiNaC::exvector | exvector_from_lst (const GiNaC::ex &l) |
| GiNaC::exvector | reverse_exvector_from_lst (const GiNaC::ex &l) |
| GiNaC::exvector | exvector_append_lst (const GiNaC::exvector &v, const GiNaC::ex &l) |
| GiNaC::exvector | exvector_multiply_last_letter (const GiNaC::exvector &v, const GiNaC::ex &x) |
| GiNaC::exvector | exvector_increase_last_degree (const GiNaC::exvector &v) |
| bool | is_class_in_nestedsums (const GiNaC::ex &expr) |
| bool | is_expr_in_sym_lst (const GiNaC::ex &expr, const GiNaC::lst &sym_lst) |
| GiNaC::ex | nestedsums_helper_normalize (const GiNaC::ex &expr, const GiNaC::lst &sym_lst=_empty_list) |
| GiNaC::ex | nestedsums_helper_sort (const GiNaC::ex &expr, const GiNaC::lst &sym_lst=_empty_list) |
| GiNaC::ex | convert_Zsums_to_standard_form (const GiNaC::ex &expr, const GiNaC::lst &sym_lst=_empty_list) |
| GINAC_BIND_UNARCHIVER (letter) | |
| GINAC_DECLARE_UNARCHIVER (letter) | |
| GiNaC::ex | create_letter (const GiNaC::ex &l, const GiNaC::ex &d) |
| GiNaC::ex | create_letter (const GiNaC::ex &l, const GiNaC::ex &d, const GiNaC::ex &i) |
| GINAC_BIND_UNARCHIVER (list_of_tgamma) | |
| GINAC_DECLARE_UNARCHIVER (list_of_tgamma) | |
| GiNaC::ex | create_list_of_tgamma (const GiNaC::ex &l) |
| GiNaC::ex | create_list_of_tgamma (const GiNaC::ex &l, const GiNaC::ex &i, const GiNaC::ex &eps, int o) |
| GiNaC::ex | create_list_of_tgamma_and_set_gammas (const GiNaC::ex &l, const GiNaC::ex &i, const GiNaC::ex &eps, int o) |
| GINAC_BIND_UNARCHIVER (multiple_polylog) | |
| ex | eval_multiple_polylog_approx (const ex &expr) |
| GINAC_DECLARE_UNARCHIVER (multiple_polylog) | |
| GiNaC::ex | create_multiple_polylog (const GiNaC::ex &llc) |
| GiNaC::ex | eval_multiple_polylog_approx (const GiNaC::ex &expr) |
| GINAC_BIND_UNARCHIVER (multiple_zeta_value) | |
| GINAC_DECLARE_UNARCHIVER (multiple_zeta_value) | |
| GiNaC::ex | create_multiple_zeta_value (const GiNaC::ex &llc) |
| GINAC_BIND_UNARCHIVER (nielsen_polylog) | |
| GINAC_DECLARE_UNARCHIVER (nielsen_polylog) | |
| GiNaC::ex | create_nielsen_polylog (const GiNaC::ex &llc) |
| GINAC_BIND_UNARCHIVER (ratio_of_tgamma) | |
| ex | eval_ratio_of_tgamma_to_scalar (const ex &expr) |
| GINAC_DECLARE_UNARCHIVER (ratio_of_tgamma) | |
| GiNaC::ex | create_ratio_of_tgamma (const GiNaC::ex &a1, const GiNaC::ex &b1, const GiNaC::ex &a2, const GiNaC::ex &b2) |
| GiNaC::ex | create_ratio_of_tgamma (const GiNaC::ex &a1, const GiNaC::ex &b1, const GiNaC::ex &a2, const GiNaC::ex &b2, const GiNaC::ex &i, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | eval_ratio_of_tgamma_to_scalar (const GiNaC::ex &expr) |
| GINAC_BIND_UNARCHIVER (root_of_unity) | |
| GINAC_DECLARE_UNARCHIVER (root_of_unity) | |
| GiNaC::ex | create_root_of_unity (unsigned l, unsigned k) |
| GINAC_BIND_UNARCHIVER (Ssum) | |
| ex | shuffle_Ssum (const ex &Z1, const ex &Z2) |
| ex | convert_Ssum_to_Zsum (const ex &Z1) |
| ex | create_Ssum_from_exvector (const ex &nc, const exvector &v) |
| ex | Ssum_to_Zsum (const ex &expr) |
| ex | shift_upper_limit_plus_one_for_Ssum (const ex &expr) |
| ex | remove_negative_degrees_from_Ssum (const ex &expr) |
| ex | remove_trivial_Ssum (const ex &expr) |
| ex | refine_Ssum (const ex &expr, unsigned q) |
| GINAC_DECLARE_UNARCHIVER (Ssum) | |
| GiNaC::ex | create_Ssum (const GiNaC::ex &nc, const GiNaC::ex &llc) |
| GiNaC::ex | shuffle_Ssum (const GiNaC::ex &Z1, const GiNaC::ex &Z2) |
| GiNaC::ex | convert_Ssum_to_Zsum (const GiNaC::ex &Z1) |
| GiNaC::ex | create_Ssum_from_exvector (const GiNaC::ex &nc, const GiNaC::exvector &v) |
| GiNaC::ex | Ssum_to_Zsum (const GiNaC::ex &expr) |
| GiNaC::ex | shift_upper_limit_plus_one_for_Ssum (const GiNaC::ex &expr) |
| GiNaC::ex | remove_negative_degrees_from_Ssum (const GiNaC::ex &expr) |
| GiNaC::ex | remove_trivial_Ssum (const GiNaC::ex &expr) |
| GiNaC::ex | refine_Ssum (const GiNaC::ex &expr, unsigned q) |
| GINAC_BIND_UNARCHIVER (Ssum_to_Infinity) | |
| GINAC_DECLARE_UNARCHIVER (Ssum_to_Infinity) | |
| GiNaC::ex | create_Ssum_to_Infinity (const GiNaC::ex &llc) |
| const symbol | symbol_factory (const std::string &symbol_name, const std::string &latex_name) |
| const symbol | next_index (void) |
| const symbol | next_x (void) |
| GINAC_BIND_UNARCHIVER (transcendental_fct_type_A) | |
| GINAC_DECLARE_UNARCHIVER (transcendental_fct_type_A) | |
| GiNaC::ex | create_transcendental_fct_type_A (const GiNaC::ex &xx, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom) |
| GiNaC::ex | create_transcendental_fct_type_A (const GiNaC::ex &xx, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom, const GiNaC::ex &eps, int o, int f) |
| GINAC_BIND_UNARCHIVER (transcendental_fct_type_B) | |
| GINAC_DECLARE_UNARCHIVER (transcendental_fct_type_B) | |
| GiNaC::ex | create_transcendental_fct_type_B (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &jj_num, const GiNaC::ex &jj_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom) |
| GiNaC::ex | create_transcendental_fct_type_B (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &jj_num, const GiNaC::ex &jj_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom, const GiNaC::ex &eps, int o, int f) |
| GINAC_BIND_UNARCHIVER (transcendental_fct_type_C) | |
| GINAC_DECLARE_UNARCHIVER (transcendental_fct_type_C) | |
| GiNaC::ex | create_transcendental_fct_type_C (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom) |
| GiNaC::ex | create_transcendental_fct_type_C (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom, const GiNaC::ex &eps, int o, int f) |
| GINAC_BIND_UNARCHIVER (transcendental_fct_type_D) | |
| GINAC_DECLARE_UNARCHIVER (transcendental_fct_type_D) | |
| GiNaC::ex | create_transcendental_fct_type_D (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &jj_num, const GiNaC::ex &jj_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom) |
| GiNaC::ex | create_transcendental_fct_type_D (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &jj_num, const GiNaC::ex &jj_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom, const GiNaC::ex &eps, int o, int f) |
| GINAC_BIND_UNARCHIVER (transcendental_sum_type_A) | |
| ex | create_transcendental_sum_type_A_and_expand (const ex &nn, const ex &i, const ex &l, const ex &v, const ex &ss, const ex &eps, int o) |
| GINAC_DECLARE_UNARCHIVER (transcendental_sum_type_A) | |
| GiNaC::ex | create_transcendental_sum_type_A (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_A_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_A_and_expand (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o) |
| GINAC_BIND_UNARCHIVER (transcendental_sum_type_B) | |
| ex | create_transcendental_sum_type_B_and_expand (const ex &nn, const ex &i, const ex &l, const ex &lr, const ex &v, const ex &vr, const ex &ss, const ex &ssr, const ex &eps, int o) |
| GINAC_DECLARE_UNARCHIVER (transcendental_sum_type_B) | |
| GiNaC::ex | create_transcendental_sum_type_B (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_B_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_B_and_expand (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o) |
| GINAC_BIND_UNARCHIVER (transcendental_sum_type_C) | |
| ex | create_transcendental_sum_type_C_and_expand (const ex &nn, const ex &i, const ex &l, const ex &v, const ex &ss, const ex &eps, int o) |
| GINAC_DECLARE_UNARCHIVER (transcendental_sum_type_C) | |
| GiNaC::ex | create_transcendental_sum_type_C (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_C_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_C_and_expand (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o) |
| GINAC_BIND_UNARCHIVER (transcendental_sum_type_D) | |
| ex | create_transcendental_sum_type_D_and_expand (const ex &nn, const ex &i, const ex &l, const ex &lr, const ex &v, const ex &vr, const ex &ss, const ex &ssr, const ex &eps, int o) |
| GINAC_DECLARE_UNARCHIVER (transcendental_sum_type_D) | |
| GiNaC::ex | create_transcendental_sum_type_D (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_D_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_D_and_expand (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o) |
| GINAC_BIND_UNARCHIVER (unit_letter) | |
| GINAC_DECLARE_UNARCHIVER (unit_letter) | |
| GiNaC::ex | create_unit_letter (const GiNaC::ex &d) |
| GiNaC::ex | create_unit_letter (const GiNaC::ex &d, const GiNaC::ex &i) |
| unsigned | rotate_left_31 (unsigned n) |
| unsigned | golden_ratio_hash (unsigned n) |
| static unsigned | make_hash_seed (const std::type_info &tinfo) |
| GINAC_BIND_UNARCHIVER (Zsum) | |
| ex | shuffle_Zsum (const ex &Z1, const ex &Z2) |
| ex | convert_Zsum_to_Ssum (const ex &Z1) |
| ex | create_Zsum_from_exvector (const ex &nc, const exvector &v) |
| ex | Zsum_to_Ssum (const ex &expr) |
| ex | shift_upper_limit_plus_one_for_Zsum (const ex &expr) |
| ex | remove_negative_degrees_from_Zsum (const ex &expr) |
| ex | remove_trivial_Zsum (const ex &expr) |
| GINAC_DECLARE_UNARCHIVER (Zsum) | |
| GiNaC::ex | create_Zsum (const GiNaC::ex &nc, const GiNaC::ex &llc) |
| GiNaC::ex | shuffle_Zsum (const GiNaC::ex &Z1, const GiNaC::ex &Z2) |
| GiNaC::ex | convert_Zsum_to_Ssum (const GiNaC::ex &Z1) |
| GiNaC::ex | create_Zsum_from_exvector (const GiNaC::ex &nc, const GiNaC::exvector &v) |
| GiNaC::ex | Zsum_to_Ssum (const GiNaC::ex &expr) |
| GiNaC::ex | shift_upper_limit_plus_one_for_Zsum (const GiNaC::ex &expr) |
| GiNaC::ex | remove_negative_degrees_from_Zsum (const GiNaC::ex &expr) |
| GiNaC::ex | remove_trivial_Zsum (const GiNaC::ex &expr) |
Variables | |
| const int | nestedsums_version_major = NESTEDSUMS_MAJOR |
| const int | nestedsums_version_minor = NESTEDSUMS_MINOR |
| const int | nestedsums_version_micro = NESTEDSUMS_MICRO |
| int | _debug_level = 0 |
| int | _nestedsums_evaluation_veto = expand_status::zombie |
| int | _nestedsums_evaluation_veto_type_A = expand_status::zombie |
| int | _nestedsums_evaluation_veto_type_B = expand_status::zombie |
| int | _nestedsums_evaluation_veto_type_C = expand_status::zombie |
| int | _nestedsums_evaluation_veto_type_D = expand_status::zombie |
| int | _NMAX = 10 |
| int | _print_format = 0 |
| const lst | _empty_list = lst() |
| const unit_letter | _unit_zero_letter = unit_letter((ex) 0) |
| const unit_letter | _unit_one_letter = unit_letter((ex) 1) |
| const list_of_tgamma | _empty_list_of_tgamma = list_of_tgamma() |
| const basic_letter | _default_basic_letter = basic_letter() |
| const Zsum | _default_Zsum = Zsum() |
| const multiple_polylog | _default_multiple_polylog = multiple_polylog() |
| const Ssum | _default_Ssum = Ssum() |
| const Ssum_to_Infinity | _default_Ssum_to_Infinity = Ssum_to_Infinity() |
| std::map< unsigned, ex > | _table_list_of_tgamma |
| int | _flag_table_list_of_tgamma = 1 |
| int | _count_table_list_of_tgamma = 0 |
| std::map< unsigned, ex > | _table_transcendental_sum_type_A |
| int | _flag_table_transcendental_sum_type_A = 1 |
| int | _count_table_transcendental_sum_type_A = 0 |
| std::map< unsigned, ex > | _table_transcendental_sum_type_C |
| int | _flag_table_transcendental_sum_type_C = 1 |
| int | _count_table_transcendental_sum_type_C = 0 |
| const GiNaC::symbol | Infinity |
| const int | add_precedence = 40 |
| const int | mul_precedence = 50 |
| const int | pow_precedence = 60 |
| const GiNaC::symbol | _default |
| const GiNaC::symbol | _default_index |
| const int | version_major = NESTEDSUMS_MAJOR |
| const int | version_minor = NESTEDSUMS_MINOR |
| const int | version_micro = NESTEDSUMS_MICRO |
Detailed Description
All classes and functions of the nestedsums package are defined in the nestedsums namespace.
Function Documentation
◆ _default()
|
extern |
A global constant to represent an unspecified symbol, used in default ctors.
◆ _default_index()
|
extern |
A global constant to represent an unspecified summation index
◆ concat()
| GiNaC::ex concat | ( | const basic_letter & | l1, |
| const basic_letter & | l2 ) |
Concat two letters.
◆ convert_Bsum_to_Ssum()
| ex convert_Bsum_to_Ssum | ( | const ex & | C | ) |
Functional form for the conversion to a Ssum.
◆ convert_Bsum_to_Zsum()
| ex convert_Bsum_to_Zsum | ( | const ex & | C | ) |
Functional form for the conversion to a Zsum.
◆ convert_Csum_to_Ssum()
| ex convert_Csum_to_Ssum | ( | const ex & | C | ) |
Functional form for the conversion to a Ssum.
◆ convert_Csum_to_Zsum()
| ex convert_Csum_to_Zsum | ( | const ex & | C | ) |
Functional form for the conversion to a Zsum.
◆ convert_Ssum_to_Zsum()
| ex convert_Ssum_to_Zsum | ( | const ex & | Z1 | ) |
Functional form for the conversion to a Ssum.
◆ convert_Zsum_to_Ssum()
| ex convert_Zsum_to_Ssum | ( | const ex & | Z1 | ) |
Functional form for the conversion to a Ssum.
◆ convert_Zsums_to_standard_form()
| ex convert_Zsums_to_standard_form | ( | const ex & | expr, |
| const lst & | sym_lst ) |
Converts an expression involving Zsums to a standard form by first removing sums with non-positive degrees, expanding the expression and bringing the coefficients to normal form.
The result is in "normal" form.
◆ create_basic_letter() [1/2]
|
inline |
Named ctor on the heap.
◆ create_basic_letter() [2/2]
|
inline |
Named ctor on the heap.
◆ create_Bsum()
|
inline |
Named ctor on the heap.
◆ create_Bsum_from_exvector()
| ex create_Bsum_from_exvector | ( | const ex & | nc, |
| const exvector & | v ) |
Construct a Bsum on the heap from an exvector.
◆ create_classical_polylog()
|
inline |
Named ctor on the heap.
◆ create_Csum()
|
inline |
Named ctor on the heap.
◆ create_Csum_from_exvector()
| ex create_Csum_from_exvector | ( | const ex & | nc, |
| const exvector & | v ) |
Construct a Csum on the heap from an exvector.
◆ create_Euler_Zagier_sum()
|
inline |
Named ctor on the heap.
◆ create_Euler_Zagier_sum_from_exvector()
| ex create_Euler_Zagier_sum_from_exvector | ( | const ex & | nc, |
| const exvector & | v ) |
Construct a Euler_Zagier_sum on the heap from an exvector.
◆ create_Euler_Zagier_sum_with_ones()
| ex create_Euler_Zagier_sum_with_ones | ( | const ex & | n, |
| const int & | k ) |
Named ctor on the heap. Creates Z_{11...1}(n) with 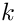
◆ create_harmonic_polylog()
|
inline |
Named ctor on the heap.
◆ create_harmonic_sum()
|
inline |
Named ctor on the heap.
◆ create_harmonic_sum_from_exvector()
| ex create_harmonic_sum_from_exvector | ( | const ex & | nc, |
| const exvector & | v ) |
Construct a harmonic_sum on the heap from an exvector.
◆ create_harmonic_sum_to_Infinity()
|
inline |
Named ctor on the heap.
◆ create_harmonic_sum_with_ones()
| ex create_harmonic_sum_with_ones | ( | const ex & | n, |
| const int & | k ) |
Named ctor on the heap. Creates S_{11...1}(n) with 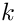
◆ create_hash_entry()
|
inline |
Named ctor on the heap.
◆ create_letter() [1/2]
|
inline |
Named ctor on the heap.
◆ create_letter() [2/2]
|
inline |
Named ctor on the heap.
◆ create_list_of_tgamma() [1/2]
|
inline |
Named ctor on the heap.
◆ create_list_of_tgamma() [2/2]
|
inline |
Named ctor on the heap.
◆ create_list_of_tgamma_and_set_gammas()
|
inline |
Named ctor on the heap.
◆ create_multiple_polylog()
|
inline |
Named ctor on the heap.
◆ create_multiple_zeta_value()
|
inline |
Named ctor on the heap.
◆ create_nielsen_polylog()
|
inline |
Named ctor on the heap.
◆ create_ratio_of_tgamma() [1/2]
|
inline |
Named ctor on the heap.
◆ create_ratio_of_tgamma() [2/2]
|
inline |
Named ctor on the heap.
◆ create_root_of_unity()
|
inline |
Named ctor on the heap.
◆ create_Ssum()
|
inline |
Named ctor on the heap.
◆ create_Ssum_from_exvector()
| ex create_Ssum_from_exvector | ( | const ex & | nc, |
| const exvector & | v ) |
Construct a Ssum on the heap from an exvector.
◆ create_Ssum_to_Infinity()
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_A() [1/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_A() [2/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_B() [1/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_B() [2/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_C() [1/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_C() [2/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_D() [1/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_fct_type_D() [2/2]
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_A()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_A_and_expand()
| ex create_transcendental_sum_type_A_and_expand | ( | const ex & | nn, |
| const ex & | i, | ||
| const ex & | l, | ||
| const ex & | v, | ||
| const ex & | ss, | ||
| const ex & | eps, | ||
| int | o ) |
Stop and go
◆ create_transcendental_sum_type_A_and_set_gammas()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_B()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_B_and_expand()
| ex create_transcendental_sum_type_B_and_expand | ( | const ex & | nn, |
| const ex & | i, | ||
| const ex & | l, | ||
| const ex & | lr, | ||
| const ex & | v, | ||
| const ex & | vr, | ||
| const ex & | ss, | ||
| const ex & | ssr, | ||
| const ex & | eps, | ||
| int | o ) |
Stop and go
◆ create_transcendental_sum_type_B_and_set_gammas()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_C()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_C_and_expand()
| ex create_transcendental_sum_type_C_and_expand | ( | const ex & | nn, |
| const ex & | i, | ||
| const ex & | l, | ||
| const ex & | v, | ||
| const ex & | ss, | ||
| const ex & | eps, | ||
| int | o ) |
Stop and go
◆ create_transcendental_sum_type_C_and_set_gammas()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_D()
|
inline |
Named ctor on the heap.
◆ create_transcendental_sum_type_D_and_expand()
| ex create_transcendental_sum_type_D_and_expand | ( | const ex & | nn, |
| const ex & | i, | ||
| const ex & | l, | ||
| const ex & | lr, | ||
| const ex & | v, | ||
| const ex & | vr, | ||
| const ex & | ss, | ||
| const ex & | ssr, | ||
| const ex & | eps, | ||
| int | o ) |
Stop and go
◆ create_transcendental_sum_type_D_and_set_gammas()
|
inline |
Named ctor on the heap.
◆ create_unit_letter() [1/2]
|
inline |
Named ctor on the heap.
◆ create_unit_letter() [2/2]
|
inline |
Named ctor on the heap.
◆ create_Zsum()
|
inline |
Named ctor on the heap.
◆ create_Zsum_from_exvector()
| ex create_Zsum_from_exvector | ( | const ex & | nc, |
| const exvector & | v ) |
Construct a Zsum on the heap from an exvector.
◆ eval_multiple_polylog_approx()
| ex eval_multiple_polylog_approx | ( | const ex & | expr | ) |
Evaluates an expression involving multiple polylog with a rough and brute force evaluation routine.
This is not a routine designed for performance. It only provides a simple way to check a result for a few selected points.
The method eval_approx is called for the rough numerical approximation.
◆ eval_ratio_of_tgamma_to_scalar()
| ex eval_ratio_of_tgamma_to_scalar | ( | const ex & | expr | ) |
Sets the status flag of ratio_of_tgamma objects to eval_to_scalar. Ratio_of_tgamma objects with integer index are then evaluated explicitly.
◆ exvector_append_lst()
| exvector exvector_append_lst | ( | const exvector & | v, |
| const ex & | l ) |
Returns an exvector, where the elements of the list l have been appended to the exvector v.
◆ exvector_from_lst()
| exvector exvector_from_lst | ( | const ex & | l | ) |
Takes a list lst(a1,a2,...,an) and constructs an exvector from it, e.g.
v[0] = a1
...
v[n-1] = an
◆ exvector_increase_last_degree()
| exvector exvector_increase_last_degree | ( | const exvector & | v | ) |
If v is an exvector of letters, then this function returns an exvector, where the degree of the last letter has been raised by one.
◆ exvector_multiply_last_letter()
| exvector exvector_multiply_last_letter | ( | const exvector & | v, |
| const ex & | x ) |
If v is an exvector of letters, then this function returns an exvector, where the scale of the last letter has been multiplied by x. The degree of the last letter is not changed.
◆ golden_ratio_hash()
|
inline |
Golden ratio hash function for the 31 least significant bits.
◆ Infinity()
|
extern |
A global constant to represent infinity
◆ is_class_in_nestedsums()
| bool is_class_in_nestedsums | ( | const ex & | expr | ) |
Returns true if expr is of type Zsum, Ssum, basic_letter, transcendental_sum_type_A to transcendental_sum_type_D, list_of_tgamma, ratio_of_tgamma, Bsum or Csum.
Returns false otherwise.
◆ is_expr_in_sym_lst()
| bool is_expr_in_sym_lst | ( | const ex & | expr, |
| const lst & | sym_lst ) |
Returns true if expr is a symbol (or a symbol raised to some power) contained in sym_lst.
Returns false otherwise.
◆ nestedsums_helper_arithmetic_sum_type_S()
| ex nestedsums_helper_arithmetic_sum_type_S | ( | const ex & | n, |
| const ex & | m ) |
Returns
![\[
\sum\limits_{i=1}^{n} i^m = n^m + \sum\limits_{k=0}^m \frac{B_k}{k!} \frac{m!}{(m+1-k)!} n^{m+1-k}
\]](form_98.png)
◆ nestedsums_helper_arithmetic_sum_type_Z()
| ex nestedsums_helper_arithmetic_sum_type_Z | ( | const ex & | n, |
| const ex & | m ) |
Returns
![\[
\sum\limits_{i=1}^{n-1} i^m = \sum\limits_{k=0}^m \frac{B_k}{k!} \frac{m!}{(m+1-k)!} n^{m+1-k}
\]](form_97.png)
◆ nestedsums_helper_bernoulli()
| GiNaC::ex nestedsums_helper_bernoulli | ( | int | n | ) |
Returns the n-th Bernoulli number. They are calculated as 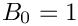
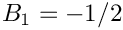
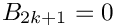
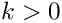
![\[
B_n = - \frac{1}{n+1} \sum\limits_{i=0}^{n-1}
\left( \begin{array}{c} n+1 \\ i \\ \end{array} \right) B_i
\]](form_94.png)
◆ nestedsums_helper_clear_hashes()
| void nestedsums_helper_clear_hashes | ( | void | ) |
Clear the hash tables
◆ nestedsums_helper_coeff()
| ex nestedsums_helper_coeff | ( | const ex & | expr, |
| const ex & | eps, | ||
| int | n ) |
Returns the coefficient of the order 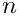
The expression is assumed to be in "expanded" or "normal" form.
◆ nestedsums_helper_eval()
| ex nestedsums_helper_eval | ( | const ex & | expr | ) |
A helper function to force the evaluation of sub-expressions.
This function distributes over the container classes add, mul, ncmul and power.
◆ nestedsums_helper_expand()
| ex nestedsums_helper_expand | ( | const ex & | expr, |
| int | level ) |
A helper routine to expand expressions. GiNaC's proper expand method is buggy, therefore we provide a method for the things we need. This helper routine knows about the classes "add", "mul" and "ncmul".
If (level & expand_request::member_variables) is true, the routine expands also recursively the arguments of the classes basic_letter, Zsum, Ssum, Csum and Bsum.
This routine is not a "complete" expand-function, for example, it does not know about the class "power" and uses in this case the native GiNaC method, if (level & expand_request::power) is set.
◆ nestedsums_helper_expand_lst_tgamma_fct()
| ex nestedsums_helper_expand_lst_tgamma_fct | ( | const ex & | ll1, |
| const ex & | ll2, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
Expands ratios of tgamma functions in eps. the first argument ll1 is a list, containing the arguments in the numerator, for example
lst( eps, 1-eps, 3+eps ).
The second argument ll2 is a list containing the arguments of the denominator. The neglected terms are of order O(eps^order).
The result is in "collected" form.
◆ nestedsums_helper_expand_power()
| ex nestedsums_helper_expand_power | ( | const ex & | x, |
| const ex & | m, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
Expands 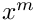
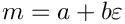
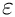
![\[
x^{a+b\varepsilon}
= x^a \sum\limits_{i=0}^\infty \varepsilon^i \frac{(-b)^i}{i!} \left( \mbox{Li}_1(1-x) \right)^i
\]](form_101.png)
The result is in expanded form.
◆ nestedsums_helper_expand_tgamma_fct()
| ex nestedsums_helper_expand_tgamma_fct | ( | const ex & | a1, |
| const ex & | b1, | ||
| const ex & | a2, | ||
| const ex & | b2, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
Expands
![\[
\frac{\Gamma(a_1+b_1 \varepsilon)}{\Gamma(a_2+b_2 \varepsilon)}
\]](form_88.png)
in 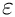
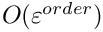
The neglected term is exactly of order 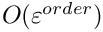
The result is in "expanded" form.
The inversion of a power series 1/( a0 + a1 eps + a2 eps^2 + ... ) sucks time and memory in GiNaC.
It is therefore more efficient to calculate the series as
![\[
\frac{1}{\Gamma(a_2+b_2 \varepsilon)} = \frac{1}{\pi} \sin \left( \pi \left( 1 - a_2 - b_2 \varepsilon \right) \right)
\Gamma(1-a_2-b_2 \varepsilon)
\]](form_89.png)
The build-in "series"-method of GiNaC does not guarantee that the neglected term is exactly of order 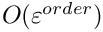
For example
expr.series(eps==0,order) works for
tgamma(1+eps),
tgamma(eps),
(1+a*eps ...)^{-1},
but does not work for
(1 + a*eps + ... + a_n eps^n),
(1/eps + a0 + a1 eps ... )^{-1}.
◆ nestedsums_helper_get_degree()
| int nestedsums_helper_get_degree | ( | const ex & | expr, |
| const ex & | eps ) |
Returns the power to which a variable appears in an expression.
On sums this function return zero, e.g. sums are not allowed to contain powers of eps.
◆ nestedsums_helper_ldegree()
| int nestedsums_helper_ldegree | ( | const ex & | expr, |
| const ex & | eps ) |
Returns the degree of the lowest order term in a Laurent series.
The expression is assumed to be in "expanded" or "normal" form.
◆ nestedsums_helper_lowering_op_geo_0()
| ex nestedsums_helper_lowering_op_geo_0 | ( | const ex & | x, |
| int | m ) |
Returns
![\[
\left( x \frac{d}{dx} \right)^m \frac{1}{1-x}
\]](form_95.png)
◆ nestedsums_helper_lowering_op_geo_1()
| ex nestedsums_helper_lowering_op_geo_1 | ( | const ex & | x, |
| int | m ) |
Returns
![\[
\left( x \frac{d}{dx} \right)^m \frac{x}{1-x}
\]](form_96.png)
◆ nestedsums_helper_multiply_laurent()
| ex nestedsums_helper_multiply_laurent | ( | const ex & | A, |
| const ex & | B, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
A routine to multiply Laurent series in eps.
A and B are Laurent series in 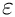
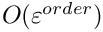
The result is in "expanded" form.
◆ nestedsums_helper_multiply_laurent_speedy()
| ex nestedsums_helper_multiply_laurent_speedy | ( | const ex & | A, |
| const ex & | B, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
As nestedsums_helper_multiply_laurent but assumes that the input is already in expanded form.
The result is in "expanded" form.
◆ nestedsums_helper_multiply_via_triangle()
| ex nestedsums_helper_multiply_via_triangle | ( | const ex & | A, |
| const ex & | B, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
A routine to multiply power series in eps.
A and B are power series in eps :
![\[
A = a_0 + a_1 \varepsilon + a_{n-1} \varepsilon^{n-1} + O(\varepsilon^n),
\]](form_82.png)
![\[
B = b_0 + b_1 \varepsilon + b_{n-1} \varepsilon^{n-1} + O(\varepsilon^n)
\]](form_83.png)
The function calculates the power series 
It does not handle the case of Laurent series, e.g. with terms like 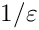
The result is in "expanded" form.
◆ nestedsums_helper_multiply_via_triangle_speedy()
| ex nestedsums_helper_multiply_via_triangle_speedy | ( | const ex & | A, |
| const ex & | B, | ||
| const ex & | expansion_parameter, | ||
| int | order ) |
As nestedsums_helper_multiply_via_triangle but assumes that the input is already in expanded form.
The result is in "expanded" form.
◆ nestedsums_helper_normalize()
| ex nestedsums_helper_normalize | ( | const ex & | expr, |
| const lst & | sym_lst ) |
This function deals with expressions of the form a1 Term1 + b1 Term2 + a2 Term1 + c1 Term3 + ..., where a1, b1, c1 are scalars and Term1, Term2 are non-commutative objects defined in this package (Zsums etc.) or products thereof.
The function combines all terms with the same Term and applies the method "normal" to them.
This function is by far more efficient than a brute force application of "normal" on the complete expression.
The result is in "normal" form.
◆ nestedsums_helper_series()
| ex nestedsums_helper_series | ( | const ex & | f, |
| const ex & | expansion_parameter, | ||
| int | order ) |
Wrapper for series expansion around expansion parameter == 0. Handles order<1 correctly.
◆ nestedsums_helper_sort()
| ex nestedsums_helper_sort | ( | const ex & | expr, |
| const lst & | sym_lst ) |
Expands an expression first and collects and normalizes terms of the same type.
The result is in "normal" form.
◆ refine_Ssum()
| ex refine_Ssum | ( | const ex & | expr, |
| unsigned | q ) |
Refines all Ssums from 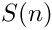
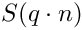
◆ remove_negative_degrees_from_Ssum()
| ex remove_negative_degrees_from_Ssum | ( | const ex & | expr | ) |
Removes non-positive degrees in Ssums.
◆ remove_negative_degrees_from_Zsum()
| ex remove_negative_degrees_from_Zsum | ( | const ex & | expr | ) |
Removes non-positive degrees in Zsums.
◆ remove_trivial_Ssum()
| ex remove_trivial_Ssum | ( | const ex & | expr | ) |
Does some trivial simplifications.
![\[
S(\infty) \rightarrow 1
\]](form_189.png)
This function has to be used with care, since 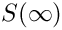
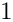
◆ remove_trivial_Zsum()
| ex remove_trivial_Zsum | ( | const ex & | expr | ) |
Does some trivial simplifications.
![\[
Z(\infty) \rightarrow 1
\]](form_347.png)
This function has to be used with care, since 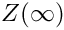
◆ reverse_exvector_from_lst()
| exvector reverse_exvector_from_lst | ( | const ex & | l | ) |
Takes a list lst(a1,a2,...,an) and constructs an exvector in the reverse order from it, e.g.
v[0] = an
...
v[n-1] = a1
◆ rotate_left_31()
|
inline |
Rotate lower 31 bits of unsigned value by one bit to the left (upper bit gets cleared).
◆ shift_upper_limit_plus_one_for_Ssum()
| ex shift_upper_limit_plus_one_for_Ssum | ( | const ex & | expr | ) |
Convert all S(n,...) appearing in the expression to S(n+1,...).
◆ shift_upper_limit_plus_one_for_Zsum()
| ex shift_upper_limit_plus_one_for_Zsum | ( | const ex & | expr | ) |
Convert all Z(n,...) appearing in the expression to Z(n+1,...).
◆ shuffle_Ssum()
| ex shuffle_Ssum | ( | const ex & | Z1, |
| const ex & | Z2 ) |
Functional form for the multiplication of two Ssums.
The method shuffle_exvector is called for the multiplication. If both sums are harmonic sums, the reimplementation of shuffle_exvector in the class harmonic_sum is used directly.
If the upper summation limits are not equal, the function returns unevaluated.
◆ shuffle_Zsum()
| ex shuffle_Zsum | ( | const ex & | Z1, |
| const ex & | Z2 ) |
Functional form for the multiplication of two Zsums.
The method shuffle_exvector is called for the multiplication. If both sums are Euler-Zagier sums, the reimplementation of shuffle_exvector in the class Euler_Zagier_sum is used directly.
If the upper summation limits are not equal, the function returns unevaluated.
◆ Ssum_to_Zsum()
| ex Ssum_to_Zsum | ( | const ex & | expr | ) |
Convert all Ssums occuring in expr into Zsums.
◆ symbol_factory()
| const GiNaC::symbol symbol_factory | ( | const std::string & | symbol_name, |
| const std::string & | latex_name ) |
The symbol factory
◆ Zsum_to_Ssum()
| ex Zsum_to_Ssum | ( | const ex & | expr | ) |
Convert all Zsums occuring in expr into Ssums.
Variable Documentation
◆ _debug_level
| int _debug_level = 0 |
A global variable which allows additional information to be printed out for debugging. If bit 0 is set, additional information during the evaluation of sums of type A is printed. If bit 1 is set, additional information during the evaluation of sums of type B is printed. If bit 2 is set, additional information during the evaluation of sums of type C is printed. If bit 3 is set, additional information during the evaluation of sums of type D is printed.
If bit 4 is set, additional information for Csum::convert_to_Ssum is printed. If bit 5 is set, additional information for Bsum::convert_to_Ssum is printed.
◆ _empty_list
|
extern |
A global variable for an empty list.
◆ _empty_list_of_tgamma
|
extern |
A global variable for an empty list of ratio_of_tgamma's.
◆ _nestedsums_evaluation_veto
| int _nestedsums_evaluation_veto = expand_status::zombie |
A global variable to stop evaluation at a certian stage
◆ _nestedsums_evaluation_veto_type_A
| int _nestedsums_evaluation_veto_type_A = expand_status::zombie |
A global variable to stop evaluation for sums of type A at a certian stage
◆ _nestedsums_evaluation_veto_type_B
| int _nestedsums_evaluation_veto_type_B = expand_status::zombie |
A global variable to stop evaluation for sums of type B at a certian stage
◆ _nestedsums_evaluation_veto_type_C
| int _nestedsums_evaluation_veto_type_C = expand_status::zombie |
A global variable to stop evaluation for sums of type C at a certian stage
◆ _nestedsums_evaluation_veto_type_D
| int _nestedsums_evaluation_veto_type_D = expand_status::zombie |
A global variable to stop evaluation for sums of type D at a certian stage
◆ _unit_one_letter
|
extern |
The unit letter of weight 1, e.g.
![\[
\frac{1}{i^1}
\]](form_29.png)
◆ _unit_zero_letter
|
extern |
ONE in the algebra of letters, e.g.
![\[
\frac{1}{i^0}
\]](form_28.png)
◆ nestedsums_version_major
| const int nestedsums_version_major = NESTEDSUMS_MAJOR |
Version information
Generated by