Fast Evolution of Parton Distributions
Public Types | Static Public Member Functions | Static Public Attributes | Static Private Member Functions | List of all members
alpha_strong Class Reference

#include <coupling.h>

Public Types

enum  { exact, truncate_in_one_over_L }
 

Static Public Member Functions

static double beta_0 (int Nf)
 
static double beta_1 (int Nf)
 
static int get_active_flavours (double Q)
 
static double get_lambda_QCD (double Q)
 
static double get_lambda_QCD (int Nf)
 
static double get_value (double Q, int Nf)
 

Static Public Attributes

static double lambda_3 = 0.374
 
static double lambda_4 = 0.327
 
static double lambda_5 = 0.226
 
static double charm_threshold = 1.3
 
static double bottom_threshold = 4.7
 
static int method = alpha_strong::truncate_in_one_over_L
 

Static Private Member Functions

static double get_F (double Q, double a_s, int Nf)
 
static double get_dF (double Q, double a_s, int Nf)
 
static double root_safeI (double a, double b, double Q, int Nf)
 

Detailed Description

The strong coupling constant.

The class works with the quantity

\[ a_s = \frac{\alpha_s}{4\pi} \]

.

If alpha_strong::method == alpha_strong::exact, the value of $a_s$ is obtained by solving numerically the equation

\[ \frac{1}{a_s} \mbox{} - \frac{\beta_1}{\beta_0} \ln \left( \beta_1 + \frac{\beta_0}{a_s} \right) \mbox{} - \beta_0 L = 0 \]

where $ L = \ln \frac{Q^2}{\Lambda^2_{QCD}}$.

If alpha_strong::method == alpha_strong::truncate_in_one_over_L, the value of $a_s$ is given by the formula

\[ a_s = \frac{1}{\beta_0 L} \left( 1 - \frac{\beta_1}{\beta_0^2} \frac{\ln L}{L} \right). \]

Member Function Documentation

§ beta_0()

double beta_0 ( int  Nf)
static

The first coefficient $\beta_0$ of the beta function

\[ \mu^2 \frac{d}{d\mu^2} a_s = - \varepsilon a_s \mbox{} - \beta_0 a_s^2 - \beta_1 a_s^3 - \beta_2 a_s^4 - ... \]

with $ a_s = \alpha_s / ( 4 \pi) $ and

\[ \beta_0 = \frac{11}{3} C_A - \frac{4}{3} T_R N_f \]

§ beta_1()

double beta_1 ( int  Nf)
static

The second coefficient $\beta_1$ of the beta function

\[ \mu^2 \frac{d}{d\mu^2} a_s = - \varepsilon a_s \mbox{} - \beta_0 a_s^2 - \beta_1 a_s^3 - \beta_2 a_s^4 - ... \]

with $ a_s = \alpha_s / ( 4 \pi) $ and

\[ \beta_1 = \frac{34}{3} C_A^2 - 4 \left( \frac{5}{3} C_A + C_F \right) T_R N_f \]

§ get_active_flavours()

int get_active_flavours ( double  Q)
static

Returns the number of active flavours at the scale 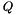$Q$.

§ get_dF()

double get_dF ( double  Q,
double  a_s,
int  Nf 
)
staticprivate

Evaluates

\[ \frac{d}{da_s} F(Q,a_s) = - \frac{\beta_0}{a_s^2} \frac{1}{(\beta_0+\beta_1 a_s)}. \]

§ get_F()

double get_F ( double  Q,
double  a_s,
int  Nf 
)
staticprivate

Evaluates

\[ F(Q,a_s) = \frac{1}{a_s} \mbox{} - \frac{\beta_1}{\beta_0} \ln \left( \beta_1 + \frac{\beta_0}{a_s} \right) \mbox{} - \beta_0 L \]

with $ L = \ln \frac{Q^2}{\Lambda^2_{QCD}}$.

§ get_lambda_QCD() [1/2]

double get_lambda_QCD ( double  Q)
static

Returns the appropriate $\Lambda_{QCD}$ corresponding to the scale $Q$.

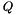§ get_lambda_QCD() [2/2]

double get_lambda_QCD ( int  Nf)
static

Returns the appropriate $\Lambda_{QCD}$ corresponding to $N_f$ active flavours.

§ get_value()

double get_value ( double  Q,
int  Nf 
)
static

Returns the value of $ a_s = \frac{\alpha_s}{4\pi}$ at the scale 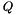$Q$ with $N_f$ active flavours.

The parameter $N_f$ ensures that the correct formula is used close to flavour thresholds.

§ root_safeI()

double root_safeI ( double  a,
double  b,
double  Q,
int  Nf 
)
staticprivate

Numerical solution of the equation

\[ \frac{1}{a_s} \mbox{} - \frac{\beta_1}{\beta_0} \ln \left( \beta_1 + \frac{\beta_0}{a_s} \right) \mbox{} - \beta_0 L = 0 \]

for $a_s$.

The documentation for this class was generated from the following files:
Generated by   doxygen 1.8.12