Fast Evolution of Parton Distributions
Classes | Typedefs | Functions | Variables
pdf Namespace Reference

Classes

class  alpha_finestruc
 
class  alpha_strong
 
class  anomalous_dimensions
 
class  evolutionkernel
 
class  integration_contour
 
class  matrix_template
 
class  partondistribution
 
class  partondistribution_with_qed
 
class  vector_template
 

Typedefs

typedef std::complex< double > complex_d
 complex numbers with double precision
 
typedef vector_template< complex_d > vector_c
 vector of complex numbers with double precision
 
typedef matrix_template< complex_d > matrix_c
 matrix of complex numbers with double precision
 
typedef vector_template< double > vector_d
 vector with double precision
 
typedef matrix_template< double > matrix_d
 matrix with double precision
 

Functions

double evolve_nonsinglet (const partondistribution &f, double Q, double x, int number_of_points)
 
double evolve_nonsinglet_3 (const partondistribution &f, double Q, double x)
 
double evolve_nonsinglet_5 (const partondistribution &f, double Q, double x)
 
double evolve_nonsinglet_10 (const partondistribution &f, double Q, double x)
 
double evolve_nonsinglet_20 (const partondistribution &f, double Q, double x)
 
double evolve_nonsinglet_30 (const partondistribution &f, double Q, double x)
 
vector_d evolve_singlet (const partondistribution &s, const partondistribution &g, double Q, double x, int number_of_points)
 
vector_d evolve_singlet_3 (const partondistribution &s, const partondistribution &g, double Q, double x)
 
vector_d evolve_singlet_5 (const partondistribution &s, const partondistribution &g, double Q, double x)
 
vector_d evolve_singlet_10 (const partondistribution &s, const partondistribution &g, double Q, double x)
 
vector_d evolve_singlet_20 (const partondistribution &s, const partondistribution &g, double Q, double x)
 
vector_d evolve_singlet_30 (const partondistribution &s, const partondistribution &g, double Q, double x)
 
vector_d evolve_singlet_with_qed (const partondistribution &Delta, const partondistribution &s, const partondistribution &g, const partondistribution &phot, const partondistribution &lept, double Q, double x, int number_of_points)
 
vector_d evolve_singlet_with_qed_3 (const partondistribution &Delta, const partondistribution &s, const partondistribution &g, const partondistribution &phot, const partondistribution &lept, double Q, double x)
 
vector_d evolve_singlet_with_qed_5 (const partondistribution &Delta, const partondistribution &s, const partondistribution &g, const partondistribution &phot, const partondistribution &lept, double Q, double x)
 
vector_d evolve_singlet_with_qed_10 (const partondistribution &Delta, const partondistribution &s, const partondistribution &g, const partondistribution &phot, const partondistribution &lept, double Q, double x)
 
vector_d evolve_singlet_with_qed_20 (const partondistribution &Delta, const partondistribution &s, const partondistribution &g, const partondistribution &phot, const partondistribution &lept, double Q, double x)
 
vector_d evolve_singlet_with_qed_30 (const partondistribution &Delta, const partondistribution &s, const partondistribution &g, const partondistribution &phot, const partondistribution &lept, double Q, double x)
 
template<class T >
vector_template< T > operator+ (const vector_template< T > &v1, const vector_template< T > &v2)
 
template<class T >
vector_template< T > operator- (const vector_template< T > &v1, const vector_template< T > &v2)
 
template<class T >
vector_template< T > operator+ (const vector_template< T > &v1)
 
template<class T >
vector_template< T > operator- (const vector_template< T > &v1)
 
template<class T , class S >
vector_template< T > operator* (const S &c, const vector_template< T > &v2)
 
template<class T , class S >
vector_template< T > operator* (const vector_template< T > &v1, const S &c)
 
template<class T , class S >
vector_template< T > operator/ (const vector_template< T > &v1, const S &c)
 
template<class T >
T operator* (const vector_template< T > &v1, const vector_template< T > &v2)
 
template<class T >
std::ostream & operator<< (std::ostream &os, const vector_template< T > &v)
 
template<class T >
matrix_template< T > operator+ (const matrix_template< T > &v1, const matrix_template< T > &v2)
 
template<class T >
matrix_template< T > operator- (const matrix_template< T > &v1, const matrix_template< T > &v2)
 
template<class T >
matrix_template< T > operator+ (const matrix_template< T > &v1)
 
template<class T >
matrix_template< T > operator- (const matrix_template< T > &v1)
 
template<class T , class S >
matrix_template< T > operator* (const S &c, const matrix_template< T > &v2)
 
template<class T , class S >
matrix_template< T > operator* (const matrix_template< T > &v1, const S &c)
 
template<class T , class S >
matrix_template< T > operator/ (const matrix_template< T > &v1, const S &c)
 
template<class T >
matrix_template< T > operator* (const matrix_template< T > &v1, const matrix_template< T > &v2)
 
template<class T >
vector_template< T > operator* (const matrix_template< T > &v1, const vector_template< T > &v2)
 
template<class T >
vector_template< T > operator* (const vector_template< T > &v1, const matrix_template< T > &v2)
 
template<class T >
std::ostream & operator<< (std::ostream &os, const matrix_template< T > &v)
 
partondistribution operator+ (const partondistribution &f1, const partondistribution &f2)
 
partondistribution_with_qed operator+ (const partondistribution_with_qed &f1, const partondistribution_with_qed &f2)
 
complex_d cot (const complex_d &xx)
 
complex_d LogSin (const complex_d &xx)
 
complex_d Gamma (const complex_d &xx)
 
complex_d LogGamma (const complex_d &xx)
 
complex_d IncompleteGamma (const complex_d &a, double x)
 
complex_d Beta (const complex_d &x, const complex_d &y)
 
complex_d HyperGeometric (const complex_d &a, const complex_d &b, const complex_d &c, const complex_d &z)
 
complex_d Psi (const complex_d &z)
 
complex_d Psi1 (const complex_d &z)
 
complex_d Psi2 (const complex_d &z)
 
complex_d Psi3 (const complex_d &z)
 
double cot (double xx)
 
double LogSin (double xx)
 
double Gamma (double xx)
 
double LogGamma (double xx)
 
double Beta (double x, double y)
 
double Psi (double z)
 
double Psi1 (double z)
 
double Psi2 (double z)
 
double Psi3 (double z)
 
complex_d S1 (const complex_d &z)
 
complex_d S2 (const complex_d &z)
 
complex_d S3 (const complex_d &z)
 
complex_d Stilde (const complex_d &z, int eta)
 
complex_d Sprim1 (const complex_d &z, int eta)
 
complex_d Sprim2 (const complex_d &z, int eta)
 
complex_d Sprim3 (const complex_d &z, int eta)
 
complex_d M1_helper (const complex_d &z)
 
complex_d M2_helper (const complex_d &z)
 

Variables

const double Pi = 3.14159265358979
 
const double Euler = 0.577215664901533
 
const double zeta2 = pow(Pi,2)/6.0
 
const double zeta3 = 1.20205690315959
 
const double Nc = 3.0
 
const double CF = 4.0/3.0
 
const double TR = 0.5
 
const double CA = 3.0
 
const double Q_up = -2.0/3.0
 
const double Q_down = 1.0/3.0
 
const double Q_electron = 1.0
 

Detailed Description

All classes and functions of the partonevolution package are defined in the namespace pdf.

Function Documentation

§ Beta() [1/2]

complex_d Beta ( const complex_d &  x,
const complex_d &  y 
)

The beta function

\[ B(x,y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} \]

§ Beta() [2/2]

double Beta ( double  x,
double  y 
)

Real version of the Beta function.

§ cot() [1/2]

complex_d cot ( const complex_d &  xx)

Cotangens

§ cot() [2/2]

double cot ( double  xx)

Real version of the cotangent function.

§ evolve_nonsinglet()

double evolve_nonsinglet ( const partondistribution &  f,
double  Q,
double  x,
int  number_of_points 
)

Entry point for the evolution of a non-singlet parton distribution.

The actual computation is passed to evolve_nonsinglet_n, where n is the number of points where the Gauss Laguerre quadrature formula is evaluated. Formulae for n = 3, 5, 10, 20 and 30 are implemented. The default choice uses 5 points.

§ evolve_nonsinglet_10()

double evolve_nonsinglet_10 ( const partondistribution &  f,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for a non-singlet parton distribution with a Gauss-Laguerre quadrature formula with 10 points.

§ evolve_nonsinglet_20()

double evolve_nonsinglet_20 ( const partondistribution &  f,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for a non-singlet parton distribution with a Gauss-Laguerre quadrature formula with 20 points.

§ evolve_nonsinglet_3()

double evolve_nonsinglet_3 ( const partondistribution &  f,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for a non-singlet parton distribution with a Gauss-Laguerre quadrature formula with 3 points.

§ evolve_nonsinglet_30()

double evolve_nonsinglet_30 ( const partondistribution &  f,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for a non-singlet parton distribution with a Gauss-Laguerre quadrature formula with 30 points.

§ evolve_nonsinglet_5()

double evolve_nonsinglet_5 ( const partondistribution &  f,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for a non-singlet parton distribution with a Gauss-Laguerre quadrature formula with 5 points.

§ evolve_singlet()

vector_d evolve_singlet ( const partondistribution &  s,
const partondistribution &  g,
double  Q,
double  x,
int  number_of_points 
)

Entry point for the evolution of singlet parton distribution. g is a parameterization of the gluon distribution, whereas s is a parameterization for

\[ \Sigma = \sum\limits_{q=u,d,...} \left( q + \bar{q} \right) \]

The actual computation is passed to evolve_nonsinglet_n, where n is the number of points where the Gauss Laguerre quadrature formula is evaluated. Formulae for n = 3, 5, 10, 20 and 30 are implemented. The default choice uses 5 points.

§ evolve_singlet_10()

vector_d evolve_singlet_10 ( const partondistribution &  s,
const partondistribution &  g,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with a Gauss-Laguerre quadrature formula with 10 points.

§ evolve_singlet_20()

vector_d evolve_singlet_20 ( const partondistribution &  s,
const partondistribution &  g,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with a Gauss-Laguerre quadrature formula with 20 points.

§ evolve_singlet_3()

vector_d evolve_singlet_3 ( const partondistribution &  s,
const partondistribution &  g,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with a Gauss-Laguerre quadrature formula with 3 points.

§ evolve_singlet_30()

vector_d evolve_singlet_30 ( const partondistribution &  s,
const partondistribution &  g,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with a Gauss-Laguerre quadrature formula with 30 points.

§ evolve_singlet_5()

vector_d evolve_singlet_5 ( const partondistribution &  s,
const partondistribution &  g,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with a Gauss-Laguerre quadrature formula with 5 points.

§ evolve_singlet_with_qed()

vector_d evolve_singlet_with_qed ( const partondistribution &  Delta,
const partondistribution &  s,
const partondistribution &  g,
const partondistribution &  phot,
const partondistribution &  lept,
double  Q,
double  x,
int  number_of_points 
)

Entry point for the evolution of the singlet parton distribution with QED effects.

The actual computation is passed to evolve_nonsinglet_n, where n is the number of points where the Gauss Laguerre quadrature formula is evaluated. Formulae for n = 3, 5, 10, 20 and 30 are implemented. The default choice uses 5 points.

§ evolve_singlet_with_qed_10()

vector_d evolve_singlet_with_qed_10 ( const partondistribution &  Delta,
const partondistribution &  s,
const partondistribution &  g,
const partondistribution &  phot,
const partondistribution &  lept,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with QED effects with a Gauss-Laguerre quadrature formula with 10 points.

§ evolve_singlet_with_qed_20()

vector_d evolve_singlet_with_qed_20 ( const partondistribution &  Delta,
const partondistribution &  s,
const partondistribution &  g,
const partondistribution &  phot,
const partondistribution &  lept,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with QED effects with a Gauss-Laguerre quadrature formula with 20 points.

§ evolve_singlet_with_qed_3()

vector_d evolve_singlet_with_qed_3 ( const partondistribution &  Delta,
const partondistribution &  s,
const partondistribution &  g,
const partondistribution &  phot,
const partondistribution &  lept,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with QED effects with a Gauss-Laguerre quadrature formula with 3 points.

§ evolve_singlet_with_qed_30()

vector_d evolve_singlet_with_qed_30 ( const partondistribution &  Delta,
const partondistribution &  s,
const partondistribution &  g,
const partondistribution &  phot,
const partondistribution &  lept,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with QED effects with a Gauss-Laguerre quadrature formula with 30 points.

§ evolve_singlet_with_qed_5()

vector_d evolve_singlet_with_qed_5 ( const partondistribution &  Delta,
const partondistribution &  s,
const partondistribution &  g,
const partondistribution &  phot,
const partondistribution &  lept,
double  Q,
double  x 
)

Evaluation of the inverse Mellin transform for singlet parton distributions with QED effects with a Gauss-Laguerre quadrature formula with 5 points.

§ Gamma() [1/2]

complex_d Gamma ( const complex_d &  xx)

The Gamma function $ \Gamma(x) $ with complex argument.

If $ \mbox{Re}(x) < 1 $ we use the reflection identity

\[ \Gamma(x) = \frac{\pi (1-x)}{\sin \left( \pi (1-x) \right)} \frac{1}{\Gamma(2-x)} \]

For $ \mbox{Re}(x) > 1 $ we use Lanczos's formula:

\[ \Gamma(x) = \left( x + \gamma_E - \frac{1}{2} \right)^{z-\frac{1}{2}} e^{- \left(x + \gamma_E - \frac{1}{2} \right)} \sqrt{2 \pi } \left[ c_0 + \frac{c_1}{x} + \frac{c_2}{x+1} + \frac{c_3}{x+3} + ... \right] \]

§ Gamma() [2/2]

double Gamma ( double  xx)

Real version of the Gamma function.

§ HyperGeometric()

complex_d HyperGeometric ( const complex_d &  a,
const complex_d &  b,
const complex_d &  c,
const complex_d &  z 
)

The hypergeometric function

\[ {}_2F_1(a,b;c;z) = \sum\limits_{n=0}^\infty \frac{(a)_n (b)_n}{(c)_n} \frac{z^n}{n!} \]

This routine approximates the hypergeometric function by the first ten terms of the series expansion.

§ IncompleteGamma()

complex_d IncompleteGamma ( const complex_d &  a,
double  x 
)

The incomplete Gamma function

\[ \Gamma(a,x) = \int\limits_x^\infty e^{-t} t^{a-1} dt, \;\;\; a>0 \]

§ LogGamma() [1/2]

complex_d LogGamma ( const complex_d &  xx)

The log of the Gamma function $ \ln \Gamma(x) $.

Since the Gamma functions grows quite fast, it's often better to calculate $ \ln \Gamma(x) $ in order to avoid overflow errors.

§ LogGamma() [2/2]

double LogGamma ( double  xx)

Real version of the LogGamma function.

§ LogSin() [1/2]

complex_d LogSin ( const complex_d &  xx)

The log of the sin function.

§ LogSin() [2/2]

double LogSin ( double  xx)

Real version of the log of the sin function.

§ M1_helper()

complex_d M1_helper ( const complex_d &  z)

The function is defined by

\[ M_1(z) = \int\limits_0^1 dx x^{z-2} \frac{\mbox{Li}_2(x)}{x+1} \]

For $ \mbox{Re} z $ large, one can use the expansion

\[ M_1(z) = \frac{1}{2} \sum\limits_{j=0}^N \left( \frac{1}{2} \right)^j \sum\limits_{l=0}^j \left( \begin{array}{c} j \\ l \\ \end{array} \right) \left( -1 \right)^l M_2(z+l) + \left( \frac{1}{2} \right)^{N+2} \zeta_2 \frac{\Gamma(N+2) \Gamma(z)}{\Gamma(z+N+2)} + {\cal O}\left( \frac{\ln z}{z^{N+3}} \right) \]

Otherwise one uses the recurrence relation

\[ M_1(z) = - M_1(z+1) + M_2(z) \]

first.

§ M2_helper()

complex_d M2_helper ( const complex_d &  z)

The function is defined by

\[ M_2(z) = \int\limits_0^1 dx x^{z-2} \mbox{Li}_2(x) = \frac{\zeta_2}{z-1} - \frac{\psi(z)-\psi(1)}{(z-1)^2} \]

§ operator*() [1/8]

vector_template<T> pdf::operator* ( const S &  c,
const vector_template< T > &  v2 
)
inline

Multiplication of a vector with a scalar:

\[ c \cdot \vec{v}_2 \]

§ operator*() [2/8]

vector_template<T> pdf::operator* ( const vector_template< T > &  v1,
const S &  c 
)
inline

Multiplication of a vector with a scalar:

\[ \vec{v}_1 \cdot c \]

§ operator*() [3/8]

T pdf::operator* ( const vector_template< T > &  v1,
const vector_template< T > &  v2 
)
inline

Scalar product of two vectors:

\[ \vec{v}_1 \cdot \vec{v}_2 \]

§ operator*() [4/8]

matrix_template<T> pdf::operator* ( const S &  c,
const matrix_template< T > &  v2 
)
inline

Multiplication of a matrix with a scalar:

\[ c \cdot A_2 \]

§ operator*() [5/8]

matrix_template<T> pdf::operator* ( const matrix_template< T > &  v1,
const S &  c 
)
inline

Multiplication of a matrix with a scalar:

\[ A_1 \cdot c \]

§ operator*() [6/8]

matrix_template<T> pdf::operator* ( const matrix_template< T > &  v1,
const matrix_template< T > &  v2 
)
inline

Multiplication of two matrices:

\[ A_1 \cdot A_2 \]

§ operator*() [7/8]

vector_template<T> pdf::operator* ( const matrix_template< T > &  v1,
const vector_template< T > &  v2 
)
inline

Multiplication of a matrix with a vector:

\[ A_1 \cdot \vec{v}_2 \]

§ operator*() [8/8]

vector_template<T> pdf::operator* ( const vector_template< T > &  v1,
const matrix_template< T > &  v2 
)
inline

Multiplication of a vector with a matrix:

\[ \vec{v}_1 \cdot A_2 \]

§ operator+() [1/6]

vector_template<T> pdf::operator+ ( const vector_template< T > &  v1,
const vector_template< T > &  v2 
)
inline

Addition of two vectors:

\[ \vec{v}_1 + \vec{v}_2 \]

§ operator+() [2/6]

vector_template<T> pdf::operator+ ( const vector_template< T > &  v1)
inline

Unary plus-operator for a vector:

\[ +\vec{v}_1 \]

§ operator+() [3/6]

partondistribution pdf::operator+ ( const partondistribution &  f1,
const partondistribution &  f2 
)

Addition of two parton distributions

The sum of two parton distributions is given by

\[ \sum\limits_{i=0}^{n-1} A_i x^{\alpha_i} (1-x)^{\beta_i} + \sum\limits_{i=0}^{n'-1} A_i' x^{\alpha_i'} (1-x)^{\beta_i'} \]

The values of 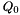$Q_0$ and $\eta$ of the two summands have to agree, otherwise the function throws an exception.

§ operator+() [4/6]

partondistribution_with_qed pdf::operator+ ( const partondistribution_with_qed &  f1,
const partondistribution_with_qed &  f2 
)

Addition of two parton distributions

The values of 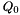$Q_0$, the electric charge and $\eta$ of the two summands have to agree, otherwise the function throws an exception.

§ operator+() [5/6]

matrix_template<T> pdf::operator+ ( const matrix_template< T > &  v1,
const matrix_template< T > &  v2 
)
inline

Addition of two matrices:

\[ A_1 + A_2 \]

§ operator+() [6/6]

matrix_template<T> pdf::operator+ ( const matrix_template< T > &  v1)
inline

Unary plus-operator for a matrix:

\[ +A_1 \]

§ operator-() [1/4]

vector_template<T> pdf::operator- ( const vector_template< T > &  v1,
const vector_template< T > &  v2 
)
inline

Subtraction of two vectors:

\[ \vec{v}_1 - \vec{v}_2 \]

§ operator-() [2/4]

vector_template<T> pdf::operator- ( const vector_template< T > &  v1)
inline

Unary minus-operator for a vector:

\[ -\vec{v}_1 \]

§ operator-() [3/4]

matrix_template<T> pdf::operator- ( const matrix_template< T > &  v1,
const matrix_template< T > &  v2 
)
inline

Subtraction of two matrices:

\[ A_1 - A_2 \]

§ operator-() [4/4]

matrix_template<T> pdf::operator- ( const matrix_template< T > &  v1)
inline

Unary minus-operator for a matrix:

\[ -A_1 \]

§ operator/() [1/2]

vector_template<T> pdf::operator/ ( const vector_template< T > &  v1,
const S &  c 
)
inline

Division of each component of a vector by a scalar:

\[ \vec{v}_1 / c \]

§ operator/() [2/2]

matrix_template<T> pdf::operator/ ( const matrix_template< T > &  v1,
const S &  c 
)
inline

Division of each component of a matrix by a scalar:

\[ A_1 / c \]

§ operator<<() [1/2]

std::ostream& pdf::operator<< ( std::ostream &  os,
const vector_template< T > &  v 
)
inline

Output operator. A vector_template prints out as [a0,a1,...,].

§ operator<<() [2/2]

std::ostream& pdf::operator<< ( std::ostream &  os,
const matrix_template< T > &  v 
)
inline

Output operator. A matrix_template prints out as [[a00,a01,...],[a10,a11,...] ... ].

§ Psi() [1/2]

complex_d Psi ( const complex_d &  z)

\[ \Psi(z) = \frac{d}{dz} \ln \Gamma(z) = \frac{1}{\Gamma(z)} \frac{d}{dz} \Gamma(z) \]

§ Psi() [2/2]

double Psi ( double  z)

Real version of the function $\Psi(z)$.

§ Psi1() [1/2]

complex_d Psi1 ( const complex_d &  z)

\[ \Psi(1,z) = \Psi'(z) = \frac{d}{dz} \Psi(z) = \frac{d^2}{dz^2} \ln \Gamma(z) \]

§ Psi1() [2/2]

double Psi1 ( double  z)

Real version of the function $\Psi(1,z)$.

§ Psi2() [1/2]

complex_d Psi2 ( const complex_d &  z)

\[ \Psi(2,z) = \Psi''(z) = \frac{d}{dz} \Psi(1,z) = \frac{d^3}{dz^3} \ln \Gamma(z) \]

§ Psi2() [2/2]

double Psi2 ( double  z)

Real version of the function $\Psi(2,z)$.

§ Psi3() [1/2]

complex_d Psi3 ( const complex_d &  z)

\[ \Psi(3,z) = \Psi'''(z) = \frac{d}{dz} \Psi(2,z) = \frac{d^4}{dz^4} \ln \Gamma(z) \]

§ Psi3() [2/2]

double Psi3 ( double  z)

Real version of the function $\Psi(3,z)$.

§ S1()

complex_d S1 ( const complex_d &  z)

Complex continuation of

\[ S_1(N) = \sum\limits_{j=1}^N \frac{1}{j} = \gamma_E + \Psi(N+1) \]

§ S2()

complex_d S2 ( const complex_d &  z)

Complex continuation of

\[ S_2(N) = \sum\limits_{j=1}^N \frac{1}{j^2} = \zeta_2 - \Psi'(N+1) \]

§ S3()

complex_d S3 ( const complex_d &  z)

Complex continuation of

\[ S_3(N) = \sum\limits_{j=1}^N \frac{1}{j^3} = \zeta_3 + \frac{1}{2} \Psi''(N+1) \]

§ Sprim1()

complex_d Sprim1 ( const complex_d &  z,
int  eta 
)

Complex continuation of

\[ S_1'(N/2) = \frac{1}{2} \left( 1 + (-1)^N \right) S_1(N/2) + \frac{1}{2} \left( 1 - (-1)^N \right) S_1((N-1)/2) \]

with $ \eta = (-1)^N $ selecting the odd or even moments.

§ Sprim2()

complex_d Sprim2 ( const complex_d &  z,
int  eta 
)

Complex continuation of

\[ S_2'(N/2) = \frac{1}{2} \left( 1 + (-1)^N \right) S_2(N/2) + \frac{1}{2} \left( 1 - (-1)^N \right) S_2((N-1)/2) \]

with $ \eta = (-1)^N $ selecting the odd or even moments.

§ Sprim3()

complex_d Sprim3 ( const complex_d &  z,
int  eta 
)

Complex continuation of

\[ S_3'(N/2) = \frac{1}{2} \left( 1 + (-1)^N \right) S_3(N/2) + \frac{1}{2} \left( 1 - (-1)^N \right) S_3((N-1)/2) \]

with $ \eta = (-1)^N $ selecting the odd or even moments.

§ Stilde()

complex_d Stilde ( const complex_d &  z,
int  eta 
)

Complex continuation of

\[ \tilde{S}(N) = \sum\limits_{j=1}^N \frac{(-1)^j}{j^2} S_1(j) \]

with $ \eta = (-1)^N $ selecting the odd or even moments.

Generated by   doxygen 1.8.12