#include <partondistribution.h>

Public Member Functions | |
| partondistribution (void) | |
| partondistribution (int n, double Q0, double A[], double alpha[], double beta[], int eta=1) | |
| partondistribution (int n, double Q0, const std::valarray< double > &A, const std::valarray< double > &alpha, const std::valarray< double > &beta, int eta=1) | |
| double | get_Q0 (void) const |
| int | get_eta (void) const |
| complex_d | get_Mellin_transform (complex_d z) const |
| double | get_F (double x, double z) const |
| double | get_dF (double x, double z) const |
| double | get_ddF (double x, double z) const |
| double | get_dddF (double x, double z) const |
| double | get_c0 (double x) const |
| virtual bool | with_qed (void) const |
| virtual double | get_electric_charge (void) const |
Protected Attributes | |
| int | n |
| double | Q0 |
| std::valarray< double > | A |
| std::valarray< double > | alpha |
| std::valarray< double > | beta |
| int | eta |
Private Member Functions | |
| double | root_safeI (double a, double b, double x) const |
Friends | |
| partondistribution | operator+ (const partondistribution &f1, const partondistribution &f2) |
Detailed Description
The class partondistribution represents the parameterization of a parton distribution in the form
![\[ x f(x,Q_0^2) = \sum\limits_{i=0}^{n-1} A_i x^{\alpha_i} (1-x)^{\beta_i} \]](form_90.png)
In addition this class has a data member  , which selects odd or even moments for the evolution. The default value for
, which selects odd or even moments for the evolution. The default value for  in the constructor is
in the constructor is  , which is good for the singlet distributions and non-singlet non-valence distributions like
, which is good for the singlet distributions and non-singlet non-valence distributions like
![\[ (u+\bar{u}) - ( d + \bar{d} ), \]](form_9.png)
![\[ (u+\bar{u}) + ( d + \bar{d} ) - 2 ( s + \bar{s} ), ... \]](form_10.png)
Valence non-singlet distributions like
![\[ (u-\bar{u}), (d - \bar{d}), ... \]](form_7.png)
need  , which has to passed explicitly to the constructor.
, which has to passed explicitly to the constructor.
Constructor & Destructor Documentation
§ partondistribution() [1/3]
| partondistribution | ( | void | ) |
Default constructor
§ partondistribution() [2/3]
| partondistribution | ( | int | nr, |
| double | Q0r, | ||
| double | Ar[], | ||
| double | alphar[], | ||
| double | betar[], | ||
| int | etar = 1 |
||
| ) |
Standard constructor
§ partondistribution() [3/3]
| partondistribution | ( | int | nr, |
| double | Q0r, | ||
| const std::valarray< double > & | Ar, | ||
| const std::valarray< double > & | alphar, | ||
| const std::valarray< double > & | betar, | ||
| int | etar = 1 |
||
| ) |
Standard constructor from valarray
Member Function Documentation
§ get_c0()
| double get_c0 | ( | double | x | ) | const |
Returns for fixed  the position of the minimum in the
the position of the minimum in the  -plane of the function
-plane of the function
![\[ F(x,z) = x^{-z} \sum\limits_{i=0}^{n-1} A_i B(z+\alpha_i-1,1+\beta_i). \]](form_77.png)
on the real axis right to the rightmost pole.
§ get_dddF()
| double get_dddF | ( | double | x, |
| double | z | ||
| ) | const |
Evaluates
![\[ \frac{d^3}{dz^3} F(x,z) = \sum\limits_{i=0}^{n-1} \left( G_i''' + 3 G_i'' G_i' + G_i'^3 \right) F_i \]](form_85.png)
where
![\[ G_i''' = \Psi''(z+\alpha_i-1) - \Psi''(z+\alpha_i+\beta_i) \]](form_86.png)
§ get_ddF()
| double get_ddF | ( | double | x, |
| double | z | ||
| ) | const |
Evaluates
![\[ \frac{d^2}{dz^2} F(x,z) = \sum\limits_{i=0}^{n-1} \left( G_i'' + G_i'^2 \right) F_i \]](form_83.png)
where
![\[ G_i'' = \Psi'(z+\alpha_i-1) - \Psi'(z+\alpha_i+\beta_i) \]](form_84.png)
§ get_dF()
| double get_dF | ( | double | x, |
| double | z | ||
| ) | const |
Evaluates
![\[ \frac{d}{dz} F(x,z) = \sum\limits_{i=0}^{n-1} G_i' F_i \]](form_79.png)
where
![\[ F_i = x^{-z} A_i B(z+\alpha_i-1,1+\beta_i), \]](form_80.png)
![\[ G_i = \ln \left( x^{-z} B(z+\alpha_i-1,1+\beta_i) \right) \]](form_81.png)
![\[ G_i' = -\ln x + \Psi(z+\alpha_i-1) - \Psi(z+\alpha_i+\beta_i) \]](form_82.png)
§ get_electric_charge()
|
inlinevirtual |
Return zero for a partondistribution. The method is overridden by the derived class partondistribution_with_qed.
Reimplemented in partondistribution_with_qed.
§ get_eta()
| int get_eta | ( | void | ) | const |
Returns  .
.
§ get_F()
| double get_F | ( | double | x, |
| double | z | ||
| ) | const |
Evaluates the function
![\[ F(x,z) = x^{-z} \sum\limits_{i=0}^{n-1} A_i B(z+\alpha_i-1,1+\beta_i). \]](form_77.png)
for the given pair  .
.
§ get_Mellin_transform()
Evaluates the Mellin transform of the parton distribution
![\[ f^z(Q_0^2) = \sum\limits_{i=0}^{n-1} A_i B(z+\alpha_i-1,1+\beta_i) \]](form_75.png)
at the point  .
.
§ get_Q0()
| double get_Q0 | ( | void | ) | const |
Returns 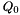 .
.
§ root_safeI()
|
private |
Solves numerically the equation
![\[ \frac{d}{dz} F(x,z) = 0 \]](form_88.png)
for  .
.
§ with_qed()
|
inlinevirtual |
Return false for a partondistribution. The method is overridden by the derived class partondistribution_with_qed.
Reimplemented in partondistribution_with_qed.
Friends And Related Function Documentation
§ operator+
|
friend |
Addition of two parton distributions
The sum of two parton distributions is given by
![\[ \sum\limits_{i=0}^{n-1} A_i x^{\alpha_i} (1-x)^{\beta_i} + \sum\limits_{i=0}^{n'-1} A_i' x^{\alpha_i'} (1-x)^{\beta_i'} \]](form_89.png)
The values of 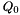 and
and  of the two summands have to agree, otherwise the function throws an exception.
of the two summands have to agree, otherwise the function throws an exception.
The documentation for this class was generated from the following files:
 1.8.12
1.8.12