#include <integrand.h>
Public Member Functions | |
| integrand () | |
| integrand (const std::vector< size_t > &index, const std::vector< exponent > &nu, const std::vector< GiNaC::ex > &poly_list, const std::vector< exponent > &c) | |
| integrand (const std::vector< exponent > &nu, const std::vector< GiNaC::ex > &poly_list, const std::vector< exponent > &c) | |
| integrand (size_t n, const std::vector< GiNaC::ex > &poly_list, const std::vector< exponent > &c) | |
| integrand (const std::vector< size_t > &index, const std::vector< exponent > &nu, const std::vector< GiNaC::ex > &poly_list, const std::vector< exponent > &c, GiNaC::ex extra_factor) | |
| integrand (const std::vector< size_t > &index, const std::vector< exponent > &nu, GiNaC::ex extra_factor) | |
| integrand (const std::vector< exponent > &nu, const std::vector< GiNaC::ex > &poly_list, const std::vector< exponent > &c, GiNaC::ex extra_factor) | |
| integrand (size_t n, const std::vector< GiNaC::ex > &poly_list, const std::vector< exponent > &c, GiNaC::ex extra_factor) | |
| GiNaC::ex | get_integrand (const integration_data &global_data) const |
| GiNaC::ex | get_weight_factor (const integration_data &global_data) const |
| GiNaC::ex | get_polynomials (const integration_data &global_data) const |
| GiNaC::ex | get_polynomials_without_exponent (const integration_data &global_data) const |
| GiNaC::ex | get_extra_factor () const |
| bool | check_homogeneous_polynomial (size_t k, const integration_data &global_data) const |
| int | get_homogeneous_degree (size_t k, const integration_data &global_data) const |
| int | get_degree (GiNaC::ex poly, const integration_data &global_data) const |
| void | make_homogeneous (size_t k, const integration_data &global_data) |
| void | make_homogeneous (const integration_data &global_data) |
| void | restrict_to_primary_sector (size_t k, const integration_data &global_data) |
| void | restrict_to_primary_sector_cube (const multi_index_counter &index_set, const integration_data &global_data) |
| bool | check_zero (size_t k, const multi_index_ordered &index_set, const integration_data &global_data) const |
| bool | check_zero (const multi_index_ordered &index_set, const integration_data &global_data) const |
| int | get_ldegree (size_t k, const multi_index_ordered &index_set, const integration_data &global_data) const |
| int | get_ldegree (const multi_index_ordered &index_set, const integration_data &global_data) const |
| GiNaC::ex | get_polyhedra_polynomial (const integration_data &global_data) const |
| bool | find_min_max (std::vector< size_t > &k_min_max_set, const integration_data &global_data) |
| bool | get_S_strategy_B (std::vector< size_t > &index_set, const integration_data &global_data) |
| bool | get_S_strategy_C (std::vector< size_t > &index_set, const integration_data &global_data) |
| void | create_subsector (size_t k, const std::vector< size_t > &index_set, const integration_data &global_data) |
| void | create_subsector (size_t k, const multi_index_ordered &index_set, const integration_data &global_data) |
| int | get_subtraction_vector (std::vector< size_t > &subtr_vec, std::vector< size_t > &index_set) const |
| GiNaC::ex | taylor_term (GiNaC::ex polynomials, const multi_index_counter_indv &counter, const std::vector< size_t > &index_set, const integration_data &global_data) const |
| void | integrated_taylor_term (const multi_index_counter_indv &counter, const std::vector< size_t > &index_set, const integration_data &global_data) |
Public Attributes | |
| std::vector< size_t > | index |
| a vector, serving as an index for integration_data::list_feynman_parameter | |
| std::vector< exponent > | weight |
| a vector holding the exponents of the single factors | |
| std::vector< GiNaC::ex > | polynomial_list |
| a vector holding the | |
| std::vector< exponent > | poly_exponent |
| a vector holding the exponents of the polynomials | |
| GiNaC::ex | extra_factor |
| an extra prefactor | |
Friends | |
| std::ostream & | operator<< (std::ostream &os, const integrand &arg) |
Detailed Description
The class integrand defines an integrand of the form
![\[
C \left( \prod\limits_{i=1}^k x_i^{\nu_0+\nu_1 \varepsilon } \right)
\left[ \prod\limits_{j=1}^r \left( P_j(x) \right)^{c_0+ c_1 \varepsilon} \right].
\]](form_20.png)
The data members are:
- std::vector<size_t> index: A vector of size
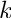
- std::vector<exponent> weight: A vector holding the exponents of the single factors
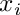
- std::vector<GiNaC::ex> polynomial_list: A vector holding the
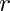
- std::vector<exponent> poly_exponent: A vector holding the exponents of the polynomials.
- GiNaC::ex extra_factor: An extra prefactor
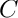
Constructor & Destructor Documentation
◆ integrand() [1/8]
| integrand | ( | ) |
Constructor.
◆ integrand() [2/8]
| integrand | ( | const std::vector< size_t > & | arg_index, |
| const std::vector< exponent > & | nu, | ||
| const std::vector< GiNaC::ex > & | poly_list, | ||
| const std::vector< exponent > & | c | ||
| ) |
Constructor.
index is initialised with arg_index, weight is initialised with nu, polynomial_list is initialised with poly_list, poly_exponent is initialised with c.
extra_factor is initialised with 1.
◆ integrand() [3/8]
| integrand | ( | const std::vector< exponent > & | nu, |
| const std::vector< GiNaC::ex > & | poly_list, | ||
| const std::vector< exponent > & | c | ||
| ) |
Constructor.
weight is initialised with nu, polynomial_list is initialised with poly_list, poly_exponent is initialised with c.
extra_factor is initialised with 1, index is initialised with (0,1,2,...)
◆ integrand() [4/8]
| integrand | ( | size_t | n, |
| const std::vector< GiNaC::ex > & | poly_list, | ||
| const std::vector< exponent > & | c | ||
| ) |
Constructor.
polynomial_list is initialised with poly_list, poly_exponent is initialised with c.
extra_factor is initialised with 1, index is initialised with (0,1,2,...,n-1), weight is initialised with n copies of exponent(0,0).
◆ integrand() [5/8]
| integrand | ( | const std::vector< size_t > & | arg_index, |
| const std::vector< exponent > & | nu, | ||
| const std::vector< GiNaC::ex > & | poly_list, | ||
| const std::vector< exponent > & | c, | ||
| GiNaC::ex | arg_extra_factor | ||
| ) |
Constructor.
index is initialised with arg_index, weight is initialised with nu, polynomial_list is initialised with poly_list, poly_exponent is initialised with c. extra_factor is initialised with arg_extra_factor.
◆ integrand() [6/8]
| integrand | ( | const std::vector< size_t > & | arg_index, |
| const std::vector< exponent > & | nu, | ||
| GiNaC::ex | arg_extra_factor | ||
| ) |
Constructor.
index is initialised with arg_index, weight is initialised with nu, extra_factor is initialised with arg_extra_factor.
polynomial_list and poly_exponent are empty.
◆ integrand() [7/8]
| integrand | ( | const std::vector< exponent > & | nu, |
| const std::vector< GiNaC::ex > & | poly_list, | ||
| const std::vector< exponent > & | c, | ||
| GiNaC::ex | arg_extra_factor | ||
| ) |
Constructor.
weight is initialised with nu, polynomial_list is initialised with poly_list, poly_exponent is initialised with c.
extra_factor is initialised with arg_extra_factor. index is initialised with (0,1,2,...)
◆ integrand() [8/8]
| integrand | ( | size_t | n, |
| const std::vector< GiNaC::ex > & | poly_list, | ||
| const std::vector< exponent > & | c, | ||
| GiNaC::ex | arg_extra_factor | ||
| ) |
Constructor.
polynomial_list is initialised with poly_list, poly_exponent is initialised with c.
extra_factor is initialised with arg_extra_factor. index is initialised with (0,1,2,...,n-1), weight is initialised with n copies of exponent(0,0).
Member Function Documentation
◆ check_homogeneous_polynomial()
| bool check_homogeneous_polynomial | ( | size_t | k, |
| const integration_data & | global_data | ||
| ) | const |
Returns true if the 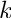
◆ check_zero() [1/2]
| bool check_zero | ( | const multi_index_ordered & | index_set, |
| const integration_data & | global_data | ||
| ) | const |
Returns true if at least one of the polynomials vanishes, when the elements of index_set are set to zero.
◆ check_zero() [2/2]
| bool check_zero | ( | size_t | k, |
| const multi_index_ordered & | index_set, | ||
| const integration_data & | global_data | ||
| ) | const |
Checks if the 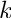
◆ create_subsector() [1/2]
| void create_subsector | ( | size_t | k, |
| const multi_index_ordered & | index_set, | ||
| const integration_data & | global_data | ||
| ) |
Creates the 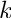
◆ create_subsector() [2/2]
| void create_subsector | ( | size_t | k, |
| const std::vector< size_t > & | index_set, | ||
| const integration_data & | global_data | ||
| ) |
Creates the 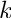
◆ find_min_max()
| bool find_min_max | ( | std::vector< size_t > & | k_min_max_set, |
| const integration_data & | global_data | ||
| ) |
Implementation of Zeillinger's strategy.
◆ get_degree()
| int get_degree | ( | GiNaC::ex | poly, |
| const integration_data & | global_data | ||
| ) | const |
Returns the degree of poly.
◆ get_extra_factor()
| GiNaC::ex get_extra_factor | ( | ) | const |
Returns the prefactor.
◆ get_homogeneous_degree()
| int get_homogeneous_degree | ( | size_t | k, |
| const integration_data & | global_data | ||
| ) | const |
Returns the homogeneous degree, if the 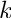
Returns 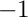
◆ get_integrand()
| GiNaC::ex get_integrand | ( | const integration_data & | global_data | ) | const |
Returns the explicit form of the integrand.
◆ get_ldegree() [1/2]
| int get_ldegree | ( | const multi_index_ordered & | index_set, |
| const integration_data & | global_data | ||
| ) | const |
Returns the ldegree of the product of all polynomials in the elements of index_set.
◆ get_ldegree() [2/2]
| int get_ldegree | ( | size_t | k, |
| const multi_index_ordered & | index_set, | ||
| const integration_data & | global_data | ||
| ) | const |
Returns the ldegree of the 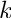
◆ get_polyhedra_polynomial()
| GiNaC::ex get_polyhedra_polynomial | ( | const integration_data & | global_data | ) | const |
Returns a polynomial, where only terms corresponding to corners of a polyhedra have been kept.
◆ get_polynomials()
| GiNaC::ex get_polynomials | ( | const integration_data & | global_data | ) | const |
Returns the explicit form of the polynomials.
◆ get_polynomials_without_exponent()
| GiNaC::ex get_polynomials_without_exponent | ( | const integration_data & | global_data | ) | const |
Returns the explicit form of the polynomials without the exponent.
The polynomial is returned in expanded form.
◆ get_S_strategy_B()
| bool get_S_strategy_B | ( | std::vector< size_t > & | index_set, |
| const integration_data & | global_data | ||
| ) |
Determines a subset of Feynman parameters accoriding to Spivakovsky's strategy.
◆ get_S_strategy_C()
| bool get_S_strategy_C | ( | std::vector< size_t > & | index_set, |
| const integration_data & | global_data | ||
| ) |
Determines a subset of Feynman parameters accoriding to strategy C.
◆ get_subtraction_vector()
| int get_subtraction_vector | ( | std::vector< size_t > & | subtr_vec, |
| std::vector< size_t > & | index_set | ||
| ) | const |
The routine fills a vector, indicating how many subtractions are needed for each variable. The indices for the corresponding variables are stored in index_set. If no subtractions are needed, the corresponding entry is not included. The return value is the number of variables, in which subtractions are needed.
◆ get_weight_factor()
| GiNaC::ex get_weight_factor | ( | const integration_data & | global_data | ) | const |
Returns the explicit form of the weight factor.
◆ integrated_taylor_term()
| void integrated_taylor_term | ( | const multi_index_counter_indv & | counter, |
| const std::vector< size_t > & | index_set, | ||
| const integration_data & | global_data | ||
| ) |
Returns one term in the Taylor expansion, integrated over the singular variables.
◆ make_homogeneous() [1/2]
| void make_homogeneous | ( | const integration_data & | global_data | ) |
Transforms all polynomials into homogeneous polynomials.
◆ make_homogeneous() [2/2]
| void make_homogeneous | ( | size_t | k, |
| const integration_data & | global_data | ||
| ) |
Transforms the 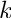
◆ restrict_to_primary_sector()
| void restrict_to_primary_sector | ( | size_t | k, |
| const integration_data & | global_data | ||
| ) |
Restricts to the 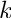
◆ restrict_to_primary_sector_cube()
| void restrict_to_primary_sector_cube | ( | const multi_index_counter & | index_set, |
| const integration_data & | global_data | ||
| ) |
Restricts to one primary sector for the integration over the standard hyper-cube.
◆ taylor_term()
| GiNaC::ex taylor_term | ( | GiNaC::ex | expr, |
| const multi_index_counter_indv & | counter, | ||
| const std::vector< size_t > & | index_set, | ||
| const integration_data & | global_data | ||
| ) | const |
Returns one term in the Taylor expansion.
Friends And Related Function Documentation
◆ operator<<
|
friend |
Output. Prints out the data of the class integrand without reference to a class integration_data.
The documentation for this class was generated from the following files: