Sector decomposition
Classes | Enumerations | Functions | Variables
sector_decomposition Namespace Reference

Classes

class  basic_multi_index
 
class  basic_sector_decomposition
 
class  exponent
 
class  integrand
 
class  integration_data
 
class  monte_carlo_parameters
 
class  monte_carlo_result
 
class  multi_index_counter
 
class  multi_index_counter_indv
 
class  multi_index_ordered
 
class  polyhedra
 

Enumerations

enum  { SIMPLEX , CUBE , CUBE_COORDINATE_SUBSPACE }
 keywords for the integration domains
 
enum  {
  STRATEGY_A , STRATEGY_B , STRATEGY_C , STRATEGY_X ,
  STRATEGY_Y
}
 keywords for the different strategies
 

Functions

monte_carlo_result do_sector_decomposition (const integration_data &global_data, const integrand &integrand_in, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
monte_carlo_result do_sector_decomposition_simplex (const integration_data &global_data, const integrand &integrand_in, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
monte_carlo_result do_sector_decomposition_cube (const integration_data &global_data, const integrand &integrand_in, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
monte_carlo_result do_sector_decomposition_cube_coordinate_subspace (const integration_data &global_data, const integrand &integrand_in, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
std::ostream & operator<< (std::ostream &os, const integration_data &arg)
 
std::ostream & operator<< (std::ostream &os, const exponent &arg)
 
std::ostream & operator<< (std::ostream &os, const integrand &arg)
 
std::string itos (int arg)
 
monte_carlo_result intnum (GiNaC::ex expr, const std::vector< GiNaC::ex > &x, const std::vector< double > &xmin, const std::vector< double > &xmax, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
monte_carlo_result intnum (GiNaC::ex expr, const std::vector< GiNaC::ex > &x, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
monte_carlo_result intnum_imp (GiNaC::ex expr, size_t dimension, double *xmin, double *xmax, const monte_carlo_parameters &mc_parameters, int verbose_level)
 
std::ostream & operator<< (std::ostream &os, const basic_multi_index &v)
 
std::ostream & operator<< (std::ostream &os, const multi_index_ordered &v)
 
std::ostream & operator<< (std::ostream &os, const multi_index_counter &v)
 
std::ostream & operator<< (std::ostream &os, const multi_index_counter_indv &v)
 
std::ostream & operator<< (std::ostream &os, const polyhedra &arg)
 

Variables

unsigned CHOICE_STRATEGY = STRATEGY_C
 global variable for the choice of the strategy
 
GiNaC::symbol Infinity = GiNaC::symbol("Infinity")
 a symbol to denote infinity
 

Detailed Description

All classes and functions of the "Sector Decomposition" package are defined in the sector_decomposition namespace.

Function Documentation

◆ do_sector_decomposition()

monte_carlo_result do_sector_decomposition ( const integration_data &  global_data,
const integrand &  integrand_in,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

The main routine to compute an integral of the form

\[ \int\limits_{x_j \ge 0} d^nx \;\delta(1-\sum_{i=1}^n x_i) \left( \prod\limits_{i=1}^n x_i^{a_i+\varepsilon b_i} \right) \prod\limits_{j=1}^r \left[ P_j(x) \right]^{c_j+\varepsilon d_j}. \]

The integration is over the standard simplex:

\[ x_j \ge 0, \;\;\; x_1+...+x_n=1. \]

For integration over the standard hyper-cube, the function do_sector_decomposition_cube can be used.

The arguments are as follows: 

  monte_carlo_result do_sector_decomposition(const integration_data & global_data,
                                             const integrand & integrand_in,
                                             const monte_carlo_parameters & mc_parameters,
                                             int verbose_level = 0);

The input are three structures, integration_data, integrand, monte_carlo_parameters, which are described in detail below, and an optional parameter verbose_level. With the help of the optional parameter verbose_level one can choose the amount of information the program prints out during the run. The function returns a structure monte_carlo_result, which again is described below.

The class integration_data contains the data which will not be modified by the algorithm for the sector decomposition. It has a constructor of the form 

 integration_data(const std::vector<GiNaC::ex> & list_feynman_parameter, 
                  GiNaC::ex epsilon, int order);

where list_feynman_parameter is a vector holding the symbols of the Feynman parameters, epsilon is the symbol of the expansion parameter and order defines which term of the Laurent series in 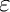$\varepsilon$ should be computed.

The integrand

\[ \left( \prod\limits_{i=1}^n x_i^{a_i+\varepsilon b_i} \right) \prod\limits_{j=1}^r \left[ P_j(x) \right]^{c_j+\varepsilon d_j} \]

is encoded in the class integrand. This class has a constructor of the form 

  integrand(const std::vector<exponent> & nu,
            const std::vector<GiNaC::ex> & poly_list, 
            const std::vector<exponent> & c);

where nu is a vector of size $n$ holding the exponents $a_i+\varepsilon b_i$. poly_list is a vector of size $r$, holding the polynomials $P_j$ in the Feynman parameters. The corresponding exponents are stored in the vector c, again of size $r$. As exponents are generally of the form $a+b\varepsilon$, a special class is available for them with the constructor 

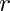
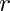
 exponent(int a, int b);

Here 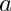$a$ and $b$ are integer numbers. Rational numbers for $a$ and $b$ are also allowed, then the constructor 

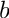
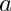
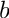
 exponent(GiNaC::ex order_0, GiNaC::ex order_1);

has to be used. In this case order_0 and order_1 have to be of type GiNaC::numeric.

In applications one encounters often integrands where the explicit powers of the Feynman parameters are missing. For integrands of the form

\[ \prod\limits_{j=1}^r \left[ P_j(x) \right]^{c_j+\varepsilon d_j} \]

there is a simpler constructor of the form 

 integrand(size_t n, const std::vector<GiNaC::ex> & poly_list, 
           const std::vector<exponent> & c);

Here, $n$ is the number of Feynman parameters.

Parameters associated to the Monte Carlo integration are specified with the help of the class monte_carlo_parameters. This class is constructed as follows: 

 monte_carlo_parameters(size_t iterations_low, size_t iterations_high, 
                        size_t calls_low, size_t calls_high);

The program uses the Vegas-algorithm based on an adaptive grid. The program does first a Monte Carlo integration with iterations_low iterations with calls_low function evaluations each. This phase is solely used to adapt the grid. The numerical result of the Monte Carlo integration is then obtained from the second stage with iterations_high iterations of calls_high function calls each.

The main function do_sector_decomposition returns the numerical results of the Monte Carlo integration in the class monte_carlo_result. This class has the methods 

 class monte_carlo_result {
  public :
   double get_mean(void) const;
   double get_error(void) const;
   double get_chi_squared(void) const;
 };

which return the mean value of the Monte Carlo integration, the error estimate and the associated 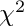$\chi^2$.

The strategy which is used for the iterated sector decomposition can be selected with the global variable sector_decomposition::CHOICE_STRATEGY. Available keywords are STRATEGY_A, STRATEGY_B, STRATEGY_C, STRATEGY_X and STRATEGY_Y. The strategies A, B and C are guaranteed to terminate. Strategies X and Y are heuristic strategies, for which there is no proof that they terminate. They are included, since in the cases where they terminate the number of generated sub-sectors tends to be smaller than the corresponding numbers for the other strategies. The default is strategy C.

The function do_sector_decomposition is just the entry point and calls the function do_sector_decomposition_simplex, which in turn delegates evaluation to a function object of type basic_sector_decomposition.

◆ do_sector_decomposition_cube()

monte_carlo_result do_sector_decomposition_cube ( const integration_data &  global_data,
const integrand &  integrand_in,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

Entry point for the integration over the standard hyper-cube.

This routine computes an integral of the form

\[ \int\limits_0^1 d^nx \; \left( \prod\limits_{i=1}^n x_i^{a_i+\varepsilon b_i} \right) \prod\limits_{j=1}^r \left[ P_j(x) \right]^{c_j+\varepsilon d_j}. \]

The integration is over the standard hyper-cube:

\[ 0 \le x_j \le 1. \]

The polynomials $P_j(x)$ are assumed to be non-vanishing inside the hyper-cube, but may vanish on the boundary of the hyper-cube. This means that the polynomials may vanish, if one or more variables $x_j$ are equal to zero or one.

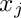
If the polynomials vanish only, if one or more variables are zero, the funtion do_sector_decomposition_cube_coordinate_subspace can be used, which is more efficient for this case.

The arguments of the function are as for the function do_sector_decomposition.

◆ do_sector_decomposition_cube_coordinate_subspace()

monte_carlo_result do_sector_decomposition_cube_coordinate_subspace ( const integration_data &  global_data,
const integrand &  integrand_in,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

Entry point for the integration over the standard hyper-cube, with singularities only on coordinate subspaces.

This routine computes an integral of the form

\[ \int\limits_0^1 d^nx \; \left( \prod\limits_{i=1}^n x_i^{a_i+\varepsilon b_i} \right) \prod\limits_{j=1}^r \left[ P_j(x) \right]^{c_j+\varepsilon d_j}. \]

The integration is over the standard hyper-cube:

\[ 0 \le x_j \le 1. \]

The polynomials $P_j(x)$ are assumed to be non-vanishing inside the hyper-cube, but may vanish on the coordinate subspaces of the hyper-cube. This means that the polynomials may vanish, if one or more variables $x_j$ are equal to zero.

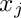
The arguments of the function are as for the function do_sector_decomposition.

◆ do_sector_decomposition_simplex()

monte_carlo_result do_sector_decomposition_simplex ( const integration_data &  global_data,
const integrand &  integrand_in,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

Entry point for the integration over the standard simplex.

The function do_sector_decomposition calls do_sector_decomposition_simplex.

The arguments of the function are as for the function do_sector_decomposition.

◆ intnum() [1/2]

monte_carlo_result intnum ( GiNaC::ex  expr,
const std::vector< GiNaC::ex > &  x,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

A simplified entry point for the Monte Carlo integration, where the integration is over the hypercube.

  • expr is the integrand,
  • x is the list of integration variables,

A simplified entry point for the Monte Carlo integration, where the integration is over the hypercube.

◆ intnum() [2/2]

monte_carlo_result intnum ( GiNaC::ex  expr,
const std::vector< GiNaC::ex > &  x,
const std::vector< double > &  xmin,
const std::vector< double > &  xmax,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

This function is the entry point for the numerical Monte Carlo integration.

  • expr is the integrand,
  • x is the list of integration variables,
  • xmin is the list of the lower integration boundaries,
  • xmax is the list of upper integration boundaries.

The entry point for the Monte Carlo integration.

◆ intnum_imp()

monte_carlo_result intnum_imp ( GiNaC::ex  expr,
size_t  dimension,
double *  xmin,
double *  xmax,
const monte_carlo_parameters &  mc_parameters,
int  verbose_level 
)

The implementation of the Monte Carlo integration.

◆ itos()

std::string itos ( int  arg)

Convert an integer into a string

◆ operator<<() [1/8]

std::ostream & operator<< ( std::ostream &  os,
const basic_multi_index &  v 
)

Output operator. A multi_index prints out as basic_multi_index( 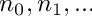$n_0,n_1,...$).

◆ operator<<() [2/8]

std::ostream & operator<< ( std::ostream &  os,
const exponent &  arg 
)

Output. Prints out the exponent in the form exponent(order_0, order_1).

◆ operator<<() [3/8]

std::ostream & operator<< ( std::ostream &  os,
const integrand &  arg 
)

Output. Prints out the data of the class integrand without reference to a class integration_data.

◆ operator<<() [4/8]

std::ostream & operator<< ( std::ostream &  os,
const integration_data &  arg 
)

Output. Prints out the Feynman parameters, the expansion parameter and the order.

◆ operator<<() [5/8]

std::ostream & operator<< ( std::ostream &  os,
const multi_index_counter &  v 
)

Output operator. A multi_index_counter prints out as multi_index_counter( 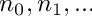$n_0,n_1,...$).

◆ operator<<() [6/8]

std::ostream & operator<< ( std::ostream &  os,
const multi_index_counter_indv &  v 
)

Output operator. A multi_index_counter_indv prints out as multi_index_counter_indv( 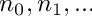$n_0,n_1,...$).

◆ operator<<() [7/8]

std::ostream & operator<< ( std::ostream &  os,
const multi_index_ordered &  v 
)

Output operator. A multi_index_ordered prints out as multi_index_ordered( 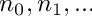$n_0,n_1,...$).

◆ operator<<() [8/8]

std::ostream & operator<< ( std::ostream &  os,
const polyhedra &  arg 
)

Output. Prints out the index vector and the coordinates.

Generated by doxygen 1.9.6