Public Member Functions |
Protected Member Functions |
Protected Attributes |
Friends |
List of all members
Csum Class Reference
Csums involve a conjugation. More...
#include <Csum.h>
Inheritance diagram for Csum:
Public Member Functions | |
| Csum (const GiNaC::ex &nc, const GiNaC::ex &llc) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | convert_to_Ssum_exvector (const GiNaC::exvector &Z1) const |
| virtual GiNaC::ex | expand_members (int level=0) const |
| GiNaC::ex | get_index (void) const |
| GiNaC::ex | get_letter_list (void) const |
| unsigned | get_depth (void) const |
Protected Member Functions | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
| virtual GiNaC::ex | decrease_letter_degree (int m) const |
| virtual GiNaC::ex | move_x0_into_x1 (void) const |
| virtual GiNaC::ex | move_x1_into_x2 (void) const |
| virtual GiNaC::ex | remove_x0 (void) const |
| virtual GiNaC::ex | remove_x0_and_x1 (void) const |
| virtual GiNaC::ex | cast_to_Bsum (void) const |
Protected Attributes | |
| GiNaC::ex | n |
| GiNaC::ex | letter_list |
Friends | |
| GiNaC::ex | convert_Csum_to_Ssum (const GiNaC::ex &C) |
| GiNaC::ex | convert_Csum_to_Zsum (const GiNaC::ex &C) |
Detailed Description
Csums involve a conjugation.
A Csum is defined by
![\[
\mbox{} - \sum\limits_{i=1}^n
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x_0^i}{i^{m_0}}
\sum\limits_{i_1=i+1}^N
\sum\limits_{i_2=i_1+1}^N ...
\sum\limits_{i_k=i_{k-1}+1}^N
\frac{x_1^{i_1}}{i_1^{m_1}}
\frac{x_2^{i_2}}{i_2^{m_2}} ...
\frac{x_k^{i_k}}{i_k^{m_k}}
\]](form_46.png)
This is equivalent to
![\[
\left( x_k^+ \right)^{m_k} \left( x_{k-1}^+ \right)^{m_{k-1}} ...
\left( x_1^+ \right)^{m_1} \left( x_0^+ \right)^{m_0}
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{x_1 ... x_k}{1-x_1 ... x_k}
\left[ 1 - \left( 1 - x_0 x_1 ... x_k \right)^n \right]
\]](form_47.png)
up to terms of the form
![\[
\left( x^+ \right)^m \frac{x}{1-x} x^N = \sum\limits_{i=N+1}^\infty \frac{x^i}{i^m}
\]](form_26.png)
Csums can be expressed in terms of Zsums or Ssums.
Basic formulae used here are:
![\[
x_1^+ \left[ 1 - \left( 1 - x_1 x_2 \right)^n \right] =
\sum\limits_{i=1}^n \frac{1}{i} \left[ 1 - \left( 1 - x_1 x_2 \right)^i \right]
\]](form_48.png)
![\[
x_1^+ \frac{x_1 x_2}{1-x_1 x_2} \left[ 1 - \left( 1 - x_0 x_1 x_2 \right)^n
\mbox{} - \left( x_1 x_2 \right)^N \left( 1 - \left( 1 - x_0 \right)^n \right) \right] =
\]](form_49.png)
![\[
= \mbox{} - \left( 1 - x_0 \right)^n \sum\limits_{i=1}^n \frac{1}{i}
\left( \frac{1}{1-x_0} \right)^i \left[ 1 - \left( 1 - x_0 x_1 x_2 \right)^i \right]
+ \left( 1 - \left( 1 - x_0 \right)^n \right) \sum\limits_{i=1}^N \frac{\left(x_1 x_2 \right)^i}{i}
\]](form_50.png)
![\[
x_1^+ \frac{x_1 x_2}{1-x_1 x_2} \left[ 1 - \left( 1 - x_1 x_2 \right)^n
\mbox{} - \left( x_1 x_2 \right)^N \right] =
\mbox{} - \frac{1}{n}
\left[ 1 - \left( 1 - x_1 x_2 \right)^n \right]
+ \sum\limits_{i=1}^N \frac{\left(x_1 x_2 \right)^i}{i}
\]](form_51.png)
Member Function Documentation
◆ cast_to_Bsum()
|
protectedvirtual |
Returns a Bsum with the same letter list and the same upper summation limit.
◆ convert_to_Ssum_exvector()
|
virtual |
◆ decrease_letter_degree()
|
protectedvirtual |
Returns a Csum where the degree of the m'th letter is decreased by one.
◆ eval()
|
override |
No automatic simplifications
◆ eval_ncmul()
|
overrideprotected |
No automatic simplifications
◆ get_depth()
|
inline |
Returns the depth.
◆ get_index()
|
inline |
Returns the upper summation limit.
◆ get_letter_list()
|
inline |
Returns the letter_list.
◆ move_x0_into_x1()
|
protectedvirtual |
Returns
![\[
\left( x_k^+ \right)^{m_k} ...
\left( \left(x_0 x_1\right)^+ \right)^{m_1}
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{x_2 ... x_k}{1-x_2 ... x_k}
\left[ 1 - \left( 1 - (x_0 x_1) ... x_k \right)^i \right]
\]](form_44.png)
◆ move_x1_into_x2()
|
protectedvirtual |
Returns
![\[
\left( x_k^+ \right)^{m_k} ...
\left( \left(x_2 x_1\right)^+ \right)^{m_2}
\left( x_0^+ \right)^{m_0} ...
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{(x_1 x_2) ... x_k}{1-(x_1 x_2) ... x_k}
\left[ 1 - \left( 1 - x_0 (x_1 x_2) ... x_k \right)^i \right]
\]](form_45.png)
◆ remove_x0()
|
protectedvirtual |
Removes x0.
◆ remove_x0_and_x1()
|
protectedvirtual |
Removes x0 and x1.
The documentation for this class was generated from the following files:
Generated by
![\[
\left( \sum\limits_{j_1=1}^{n'} \sum\limits_{j_2=1}^{j_1} ... \sum\limits_{n=1}^{j_{l-1}}
\frac{y_1^{j_1}}{j_1^{g_1}} ... \frac{y_l^{n}}{n^{g_l}} \right)
\left( x_k^+ \right)^{m_k} ...
\left( x_1^+ \right)^{m_1} \left( x_0^+ \right)^{m_0}
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{x_1 ... x_k}{1-x_1 ... x_k}
\left[ 1 - \left( 1 - x_0 x_1 ... x_k \right)^n \right]
\]](form_30.png)
![\[
\left( \sum\limits_{j_1=1}^{n'} \sum\limits_{j_2=1}^{j_1} ... \sum\limits_{n=1}^{j_{l-1}} ...
\sum\limits_{i=1}^{n} \frac{1}{i} \right)
\left( x_k^+ \right)^{m_k} ...
\left( x_1^+ \right)^{m_1} \left( x_0^+ \right)^{m_0-1}
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{x_1 ... x_k}{1-x_1 ... x_k}
\left[ 1 - \left( 1 - x_0 x_1 ... x_k \right)^i \right]
\]](form_32.png)
![\[
\left( \sum\limits_{j_1=1}^{n'} ... \sum\limits_{n=1}^{j_{l-1}} ... \right)
\mbox{} - \left( \sum\limits_{j_1=1}^{n'} ... \sum\limits_{n=1}^{j_{l-1}} ... (1-x_0)^n \right)
\]](form_35.png)
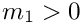
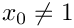
![\[
\mbox{} - \left( \sum\limits_{j_1=1}^{n'} ... (1-x_0)^n
\sum\limits_{i=1}^n \frac{1}{i} \left( \frac{1}{1-x_0} \right)^i
\left( x_k^+ \right)^{m_k} ...
\left( \left(x_0 x_1\right)^+ \right)^{m_1-1}
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{x_2 ... x_k}{1-x_2 ... x_k}
\left[ 1 - \left( 1 - (x_0 x_1) ... x_k \right)^i \right] \right)
\]](form_38.png)
![\[
\mbox{} + \left( \sum\limits_{j_1=1}^{n'} ... \right)
\sum\limits_{i_1=1}^N \frac{x_1}{i_1^{m_1}}
\sum\limits_{i_2=i_1+1}^N ... \sum\limits_{i_k=i_{k-1}+1}^N
\frac{x_2^{i_2}}{i_2^{m_2}} ... \frac{x_k^{i_k}}{i_k^{m_k}}
\]](form_39.png)
![\[
\mbox{} - \left( \sum\limits_{j_1=1}^{n'} ... (1-x_0)^n \right)
\sum\limits_{i_1=1}^N \frac{x_1}{i_1^{m_1}}
\sum\limits_{i_2=i_1+1}^N ... \sum\limits_{i_k=i_{k-1}+1}^N
\frac{x_2^{i_2}}{i_2^{m_2}} ... \frac{x_k^{i_k}}{i_k^{m_k}}
\]](form_40.png)
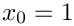
![\[
\mbox{} - \left( \sum\limits_{j_1=1}^{n'} ... \frac{1}{n} \right)
\left( x_k^+ \right)^{m_k} ...
\left( x_1^+ \right)^{m_1-1}
\frac{x_k}{1-x_k} \frac{x_{k-1}x_k}{1-x_{k-1}x_k} ...
\frac{x_2 ... x_k}{1-x_2 ... x_k}
\left[ 1 - \left( 1 - x_1 ... x_k \right)^n \right]
\]](form_42.png)
![\[
\mbox{} + \left( \sum\limits_{j_1=1}^{n'} ... \right)
\sum\limits_{i=1}^N \frac{x_1^{i}}{i^{m_1}}
\sum\limits_{i_2=i+1}^{N} ... \sum\limits_{i_k = i_{k-1}+1}^{N}
\frac{x_2^{i_2}}{i_2^{m_2}} ... \frac{x_k^{i_k}}{i_k^{m_k}}
\]](form_43.png)