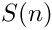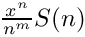Ssums form an algebra. More...
#include <Ssum.h>
Public Member Functions | |
| Ssum (const GiNaC::ex &nc) | |
| Ssum (const GiNaC::ex &nc, const GiNaC::ex &llc) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | convert_to_Zsum_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1) const |
| virtual GiNaC::ex | shuffle_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1, const GiNaC::exvector &Z2) const |
| virtual GiNaC::ex | refine_exvector (unsigned q, const GiNaC::exvector &Z0, const GiNaC::exvector &Z1) const |
| virtual GiNaC::ex | refine (unsigned q) const |
| virtual GiNaC::ex | set_index (const GiNaC::ex &i) const |
| virtual GiNaC::ex | shift_plus_one (void) const |
| virtual GiNaC::ex | shift_minus_one (void) const |
| virtual GiNaC::ex | adjust_upper_limit_downwards (const GiNaC::ex &i) const |
| virtual GiNaC::ex | adjust_upper_limit_upwards (const GiNaC::ex &i) const |
| virtual GiNaC::ex | adjust_upper_limit_plus_one (void) const |
| virtual GiNaC::ex | index_eq_one (void) const |
| virtual GiNaC::ex | get_head (int k) const |
| virtual GiNaC::ex | get_tail (int k) const |
| virtual int | flag_remove_negative_degrees (void) const |
| virtual GiNaC::ex | remove_negative_degrees (void) const |
| virtual GiNaC::ex | expand_members (int level=0) const |
| virtual GiNaC::ex | eval_explicit () const |
| virtual GiNaC::ex | get_first_letter (void) const |
| virtual GiNaC::ex | remove_first_letter (void) const |
| virtual GiNaC::ex | remove_first_letter (const GiNaC::ex &nc) const |
| virtual GiNaC::ex | prepend_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | prepend_letter (const GiNaC::ex &nc, const GiNaC::ex &lc) const |
| virtual GiNaC::ex | append_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | append_letter_list (const GiNaC::ex &lc) const |
| GiNaC::ex | get_index (void) const |
| GiNaC::ex | get_letter_list (void) const |
| unsigned | get_depth (void) const |
| GiNaC::ex | get_weight (void) const |
Protected Member Functions | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
| virtual GiNaC::ex | cast_to_Zsum (void) const |
| virtual GiNaC::ex | multiply_letter_with_last_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | multiply_letter_with_first_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | concat_two_sums (const GiNaC::ex &Z1, const GiNaC::ex &Z2) const |
Protected Attributes | |
| GiNaC::ex | n |
| GiNaC::ex | letter_list |
Friends | |
| class | Csum |
| GiNaC::ex | shuffle_Ssum (const GiNaC::ex &Z1, const GiNaC::ex &Z2) |
| GiNaC::ex | convert_Ssum_to_Zsum (const GiNaC::ex &Z1) |
| GiNaC::ex | remove_trivial_Ssum (const GiNaC::ex &expr) |
Detailed Description
Ssums form an algebra.
A Ssum is recursively defined by
![\[
S(n;m_1,...,m_k;x_1,...,x_k) = \sum\limits_{i=1}^n \frac{x_1^i}{i^{m_1}} S(i;m_2,...,m_k;x_2,...,x_k)
\]](form_192.png)
with
![\[
S(n) = 1
\]](form_193.png)
for 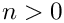
![\[
S(n) = 0
\]](form_194.png)
for 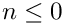
Ssums can be converted to Zsums (and vice versa).
All letters should have their index set to _default_index.
Member Function Documentation
◆ adjust_upper_limit_downwards()
|
virtual |
Adjusts the upper summation limit 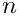
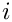
![\[
S(n;m_1,...;x_1,...) = S(i;m_1,...;x_1,...)
+ \sum\limits_{j=0}^{n-i-1} x_1^{j+1} \frac{x_1^i}{(i+j+1)^{m_1}} S(i+j+1;m_2,...;x_2,...)
\]](form_175.png)
with 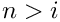
For the empty sum we have
![\[
S(n) = S(i)
\]](form_73.png)
This routine assumes 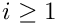
Reimplemented in harmonic_sum.
◆ adjust_upper_limit_plus_one()
|
virtual |
◆ adjust_upper_limit_upwards()
|
virtual |
Adjusts the upper summation limit 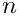
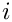
![\[
S(n;m_1,...;x_1,...) = S(i;m_1,...;x_1,...)
\mbox{} - \sum\limits_{j=0}^{i-n-1} x_1^{-j} \frac{x_1^i}{(i-j)^{m_1}} S(i-j;m_2,...;x_2,...)
\]](form_176.png)
with 
For the empty sum we have
![\[
S(n) = S(i)
\]](form_73.png)
This routine assumes 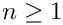
This routine might give rise to poles for some values of 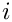
Reimplemented in harmonic_sum.
◆ append_letter()
|
virtual |
Appends the letter lc to the letter_list.
◆ append_letter_list()
|
virtual |
Appends the list lc to the letter_list.
◆ cast_to_Zsum()
|
protectedvirtual |
Creates a Zsum with the same upper summation index and the same letter_list.
This is a crude cast, something like reinterpret_cast.
◆ concat_two_sums()
|
protectedvirtual |
Takes Z1 as head and Z2 as tail and forms a new sum as the concatenation of the two.
◆ convert_to_Zsum_exvector()
|
virtual |
Method to convert a Ssum to a Zsum.
An efficient version for the conversion to Zsums, based on exvector (e.g. std::vector<GiNaC::ex> ). Z0 contains the result. Z1 is reversed order, so that we can use pop_back.
The basic formula is
![\[
S(n;m_1,...;x_1,...) = \sum\limits_{i=1}^n \frac{x_1^i}{i^{m_1}} S(i-1;m_2,...;x_2,...)
\mbox{} + S(n;m_1+m_2,...;x_1 x_2, ...)
\]](form_167.png)
Reimplemented in harmonic_sum.
◆ eval()
|
override |
The simplifications are done in the following order:
- If the upper summation limit is equal to infinity, we have a Ssum_to_Infinity
- If all
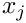
- If the upper summation index is an integer, perform the sum explicitly.
◆ eval_explicit()
|
virtual |
Explicit evaluation
◆ eval_ncmul()
|
overrideprotected |
A product of Ssums is simplified, if the last two have the same upper summation index.
A product is also simplified if the difference between the two upper summation indices is an integer. The factor with the "larger" upper summation index is converted to the "smaller" index with the help of the function Zsum::adjust_upper_limit_downwards. Note that the algorithm returns a product, where both factors have the "smaller" index.
◆ flag_remove_negative_degrees()
|
virtual |
Signals if there are letters with negative or zero degrees.
Only for Ssums.
◆ get_depth()
|
inline |
Returns the depth.
◆ get_first_letter()
|
virtual |
Returns the first letter from the letter_list.
◆ get_head()
|
virtual |
Returns from the S-sum 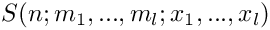
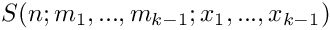
◆ get_index()
|
inline |
Returns the upper summation limit.
◆ get_letter_list()
|
inline |
Returns the letter_list.
◆ get_tail()
|
virtual |
Returns from the S-sum 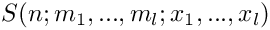
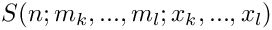
◆ get_weight()
| ex get_weight | ( | void | ) | const |
Returns the weight.
◆ index_eq_one()
|
virtual |
Returns
![\[
S(1;m_1,...,m_k;x_1,...,x_k) = x_1 \cdot ... \cdot x_k
\]](form_178.png)
◆ multiply_letter_with_first_letter()
|
protectedvirtual |
◆ multiply_letter_with_last_letter()
|
protectedvirtual |
◆ refine()
|
virtual |
Method to convert a Ssum with upper limit 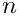
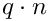
◆ refine_exvector()
|
virtual |
Helper routine to convert a Ssum with upper limit 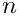
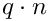
Z0 contains the result in reversed order. Z1 the letter list, which has to be converted.
The basic formula is
![\[
\sum\limits_{i=1}^n \frac{x^i}{i^m} S( q \cdot i;...)
= q^{m-1} \sum\limits_{l=0}^{q-1}
\sum\limits_{i=1}^{q \cdot n} \frac{1}{i^m}
\left( r_q^l x^{1/q} \right)^i S(i;...)
\]](form_171.png)
Here 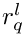
◆ remove_first_letter()
|
virtual |
Returns a Ssum with the first letter removed from the letter_list.
Reimplemented in harmonic_sum.
◆ remove_negative_degrees()
|
virtual |
Removes letters with non-positive degrees.
The basic formula is
![\[
S(n;-m_1,m_2,...;x_1,x_2,...) =
\sum\limits_{i2=1}^n \frac{x_2^{i_2}}{i_2^{m_2}} S(i_2;m_3,...;x_3,...)
\sum\limits_{i_1=i_2}^n i_1^{m_1} x_1^{i_1}
\]](form_184.png)
For 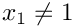
![\[
\sum\limits_{i_1=i_2}^n i_1^{m_1} x_1^{i_1} =
\left( x_1^- \right)^{m_1} \left( \frac{1}{1-x_1} x_1^{i_2} - \frac{x_1}{1-x_1} x_1^n \right)
\]](form_186.png)
For 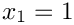
![\[
\sum\limits_{i_1=i_2}^n i_1^{m_1} =
\sum\limits_{i_1=1}^n i_1^{m_1} - \sum\limits_{i_1=1}^{i_2-1} i_1^{m_1}
\]](form_188.png)
and the sums can be done analytically with the help of the Bernoulli numbers:
![\[
\sum\limits_{i=1}^{n} i^m = n^m + \sum\limits_{k=0}^m \frac{B_k}{k!} \frac{m!}{(m+1-k)!} n^{m+1-k}
\]](form_98.png)
◆ set_index()
|
virtual |
Sets the upper summation index to 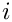
Reimplemented in harmonic_sum.
◆ shift_minus_one()
|
virtual |
Returns 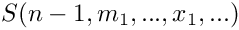
Reimplemented in harmonic_sum.
◆ shift_plus_one()
|
virtual |
Returns 
Reimplemented in harmonic_sum.
◆ shuffle_exvector()
|
virtual |
Method to multiply two Ssums.
An efficient version for the multiplication of Ssums, based on exvector (e.g. std::vector<GiNaC::ex> ). Z0 contains the result. Z1 and Z2 are in reversed order, so that we can use pop_back.
The basic formula is
![\[
S(n;m_1,...;x_1,...) S(n;m_1',...;x_1',...)
= \sum\limits_{i=1}^n \frac{x_1^i}{i^{m_1}} S(i;m_2,...;x_2,...) S(i;m_1',...;x_1',...)
\]](form_168.png)
![\[
\mbox{} + \sum\limits_{i=1}^n \frac{{x_1'}^i}{i^{m_1'}} S(i;m_1,...;x_1,...) S(i;m_2',...;x_2',...)
\mbox{} - \sum\limits_{i=1}^n \frac{(x_1 {x_1'})^i}{i^{m_1+m_1'}} S(i;m_2,...;x_2,...) S(i;m_2',...;x_2',...)
\]](form_169.png)
Note the minus sign in front of the last term.
Reimplemented in harmonic_sum.
The documentation for this class was generated from the following files:
Generated by
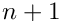
![\[
S(n;m_1,...;x_1,...) = S(n+1;m_1,...;x_1,...)
\mbox{} - \frac{x_1^{n+1}}{(n+1)^{m_1}} S(n+1;m_2,...;x_2,...).
\]](form_177.png)