Nestedsums library
Public Member Functions | Protected Member Functions | Protected Attributes | Friends | List of all members
basic_letter Class Reference

A basic_letter is an element of an alphabet. More...

#include <basic_letter.h>

Inheritance diagram for basic_letter:
letter unit_letter

Public Member Functions

 basic_letter (const GiNaC::ex &l, const GiNaC::ex &d, const GiNaC::ex &o)
 
 basic_letter (const GiNaC::ex &l, const GiNaC::ex &d, const GiNaC::ex &o, const GiNaC::ex &i)
 
void archive (GiNaC::archive_node &node) const override
 
void read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override
 
unsigned return_type (void) const override
 
void print (const GiNaC::print_context &c, unsigned level=0) const override
 
unsigned precedence (void) const override
 
GiNaC::ex eval () const override
 
GiNaC::ex subs (const GiNaC::exmap &m, unsigned options=0) const override
 
virtual GiNaC::ex concat (const GiNaC::ex &l) const
 
virtual GiNaC::ex eval_explicit () const
 
virtual GiNaC::ex expand_members (int level=0) const
 
GiNaC::ex get_scale (void) const
 
GiNaC::ex get_degree (void) const
 
GiNaC::ex get_offset (void) const
 
GiNaC::ex get_index (void) const
 
GiNaC::ex set_index (const GiNaC::ex &i) const
 
GiNaC::ex forget_index (void) const
 
GiNaC::ex shift_index (const GiNaC::ex &new_index) const
 
GiNaC::ex index_eq_one (void) const
 
GiNaC::ex shift_plus_one (void) const
 
GiNaC::ex shift_minus_one (void) const
 
GiNaC::ex degree_minus_one (void) const
 
GiNaC::ex degree_plus_one (void) const
 

Protected Member Functions

GiNaC::ex eval_ncmul (const GiNaC::exvector &v) const override
 
GiNaC::ex derivative (const GiNaC::symbol &s) const override
 
unsigned calchash (void) const override
 
virtual GiNaC::ex concat_speedy (const GiNaC::ex &l) const
 

Protected Attributes

GiNaC::ex scale
 
GiNaC::ex degree
 
GiNaC::ex offset
 
GiNaC::ex index
 

Friends

GiNaC::ex concat (const basic_letter &l1, const basic_letter &l2)
 

Detailed Description

A basic_letter is an element of an alphabet.

The model for a basic_letter is

\[ \frac{x^i}{(i+c)^m} \]

Here $x$ is the scale, $m$ the degree, $c$ the offset and $i$ a parameter (usually a summation index). $i$ does not need to be specified. In this case the index is set to the default index.

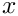
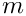
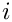
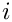
Two basic_letters can be multiplied ("concatenated") to form a new basic_letter.

Member Function Documentation

◆ concat_speedy()

ex concat_speedy ( const GiNaC::ex & l) const
protectedvirtual

Same as concat, but does not perform any checking. Assumes that the indices are the same or equal to the default one.

The multiplication is performed if the two basic_letters have

  • the same offset

    \[ \frac{x^i}{(i+c)^{m_1}} \frac{y^i}{(i+c)^{m_2}} = \frac{(xy)^i}{(i+c)^{m_1+m_2}} \]

  • unequal offsets, but both degrees are integers (and not symbols).

    If one of the degrees is zero, we have

    \[ \frac{x^i}{(i+c)^{m}} y^i = \frac{(xy)^i}{(i+c)^{m}} \]

    If both degrees are positive, we have

    \[ \frac{x^i}{(i+c_1)^{m_1}} \frac{y^i}{(i+c_2)^{m_2}} = \frac{1}{c_2-c_1} \left[ \frac{x^i}{(i+c_1)^{m_1}} \frac{y^i}{(i+c_2)^{m_2-1}} \mbox{} - \frac{x^i}{(i+c_1)^{m_1-1}} \frac{y^i}{(i+c_2)^{m_2}} \right] \]

    If one degree is positive ( $m_1$), the other negative ( $m_2$), we have

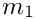
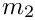
    \[ \frac{x^i}{(i+c_1)^{m_1}} \frac{y^i}{(i+c_2)^{m_2}} = \frac{x^i}{(i+c_1)^{m_1-1}} \frac{y^i}{(i+c_2)^{m_2+1}} + (c_2-c_1) \frac{x^i}{(i+c_1)^{m_1}} \frac{y^i}{(i+c_2)^{m_2+1}} \]

    Finally, if both degrees are negative, we have

    \[ \frac{x^i}{(i+c_1)^{m_1}} \frac{y^i}{(i+c_2)^{m_2}} = \frac{x^i}{(i+c_1)^{m_1-1}} \frac{y^i}{(i+c_2)^{m_2+1}} + (c_2-c_1) \frac{x^i}{(i+c_1)^{m_1}} \frac{y^i}{(i+c_2)^{m_2+1}} \]

    To avoid an infinite recursion in the last case, the algorithm does not commute two basic_letters.

The multiplication does not alter the offset, e.g. if we have 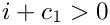$i+c_1 > 0$ and $i+c_2 > 0$ for all $i$, then the evaluated product of the two basic_letters has only the offsets $c_1$ or $c_2$. Multiplying two basic_letters does not introduce poles.

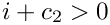
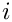
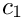
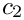
The result gets the index from the first letter, if this one differs from _default_index, otherwise the result gets the index from the second letter.

The routine returns unevaluated if

  • the offsets are not equal and at least one degree is not an integer.

Reimplemented in letter, and unit_letter.

◆ degree_minus_one()

ex degree_minus_one ( void ) const

Returns a basic_letter with degree-1

◆ degree_plus_one()

ex degree_plus_one ( void ) const

Returns a basic_letter with degree+1

◆ eval()

ex eval ( ) const
override

If the offset is zero, evaluation returns a letter .

If the index is an integer, the object is evaluated explicitly.

◆ eval_explicit()

ex eval_explicit ( ) const
virtual

Explicit evaluation.

◆ eval_ncmul()

ex eval_ncmul ( const GiNaC::exvector & v) const
overrideprotected

A product of two basic_letter's is simplified, if

  • the two indices are equal, or at least one of the indices is equal to the default index;
  • and both basic_letter's are actually of type letter;
  • or the types are only basic_letter's, but both degrees are integer.

A product is also simplified if the difference between the two indices is an integer, according to

\[ \frac{x^{i+l}}{((i+l)+c)^m} \frac{y^i}{(i+c')^{m'}} = x^l \frac{x^{i}}{(i+(c+l))^m} \frac{y^i}{(i+c')^{m'}} \]

where $ l > 0 $. Note that the algorithm returns a product, where both factors have the "smaller" index.

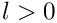
◆ forget_index()

ex forget_index ( void ) const

Sets the index to the default index.

◆ get_degree()

GiNaC::ex get_degree ( void ) const
inline

Returns the degree

◆ get_index()

GiNaC::ex get_index ( void ) const
inline

Returns the index

◆ get_offset()

GiNaC::ex get_offset ( void ) const
inline

Returns the offset

◆ get_scale()

GiNaC::ex get_scale ( void ) const
inline

Returns the scale

◆ index_eq_one()

ex index_eq_one ( void ) const

Returns

\[ \frac{x}{(1+c)^m} \]

◆ set_index()

ex set_index ( const GiNaC::ex & i) const

Sets the index to 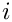$i$

◆ shift_index()

ex shift_index ( const GiNaC::ex & new_index) const

Adjusts the index according to

\[ \frac{x^j}{(j+c)^m} = x^{j-i} \frac{x^i}{(i+c+(j-i))^m} \]

◆ shift_minus_one()

ex shift_minus_one ( void ) const

Returns a basic_letter with offset-1

◆ shift_plus_one()

ex shift_plus_one ( void ) const

Returns a basic_letter with offset+1

Friends And Related Symbol Documentation

◆ concat

GiNaC::ex concat ( const basic_letter & l1,
const basic_letter & l2 )
friend

Concat two letters.

The documentation for this class was generated from the following files:
Generated by doxygen 1.12.0