A harmonic polylog is a special case of a multiple polylog. More...

#include <harmonic_polylog.h>

Inheritance diagram for harmonic_polylog:

Public Member Functions
	harmonic_polylog (const GiNaC::ex &llc)

void	archive (GiNaC::archive_node &node) const override

void	read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override

GiNaC::return_type_t	return_type_tinfo () const override

void	print (const GiNaC::print_context &c, unsigned level=0) const override

GiNaC::ex	eval () const override

Public Member Functions inherited from multiple_polylog
	multiple_polylog (const GiNaC::ex &llc)

void	archive (GiNaC::archive_node &node) const override

void	read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override

void	print (const GiNaC::print_context &c, unsigned level=0) const override

GiNaC::ex	eval () const override

virtual GiNaC::ex	eval_approx () const

Public Member Functions inherited from Zsum
	Zsum (const GiNaC::ex &nc)

	Zsum (const GiNaC::ex &nc, const GiNaC::ex &llc)

void	archive (GiNaC::archive_node &node) const override

void	read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override

unsigned	return_type (void) const override

void	print (const GiNaC::print_context &c, unsigned level=0) const override

unsigned	precedence (void) const override

GiNaC::ex	eval () const override

GiNaC::ex	subs (const GiNaC::exmap &m, unsigned options=0) const override

virtual GiNaC::ex	convert_to_Ssum_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1) const

virtual GiNaC::ex	shuffle_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1, const GiNaC::exvector &Z2) const

virtual GiNaC::ex	set_index (const GiNaC::ex &i) const

virtual GiNaC::ex	shift_plus_one (void) const

virtual GiNaC::ex	shift_minus_one (void) const

virtual GiNaC::ex	adjust_upper_limit_downwards (const GiNaC::ex &i) const

virtual GiNaC::ex	adjust_upper_limit_upwards (const GiNaC::ex &i) const

virtual GiNaC::ex	adjust_upper_limit_plus_one (void) const

virtual GiNaC::ex	index_eq_one (void) const

virtual GiNaC::ex	get_head (int k) const

virtual GiNaC::ex	get_tail (int k) const

virtual GiNaC::ex	antipode (void) const

virtual GiNaC::ex	expand_members (int level=0) const

virtual GiNaC::ex	eval_explicit () const

virtual GiNaC::ex	get_first_letter (void) const

virtual GiNaC::ex	remove_first_letter (void) const

virtual GiNaC::ex	remove_first_letter (const GiNaC::ex &nc) const

virtual GiNaC::ex	prepend_letter (const GiNaC::ex &lc) const

virtual GiNaC::ex	prepend_letter (const GiNaC::ex &nc, const GiNaC::ex &lc) const

virtual GiNaC::ex	append_letter (const GiNaC::ex &lc) const

virtual GiNaC::ex	append_letter_list (const GiNaC::ex &lc) const

GiNaC::ex	get_index (void) const

GiNaC::ex	get_letter_list (void) const

unsigned	get_depth (void) const

GiNaC::ex	get_weight (void) const

Additional Inherited Members
Protected Member Functions inherited from Zsum
GiNaC::ex	eval_ncmul (const GiNaC::exvector &v) const override

GiNaC::ex	derivative (const GiNaC::symbol &s) const override

unsigned	calchash (void) const override

virtual GiNaC::ex	cast_to_Ssum (void) const

virtual GiNaC::ex	multiply_letter_with_last_letter (const GiNaC::ex &lc) const

virtual GiNaC::ex	multiply_letter_with_first_letter (const GiNaC::ex &lc) const

virtual GiNaC::ex	concat_two_sums (const GiNaC::ex &Z1, const GiNaC::ex &Z2) const

Protected Attributes inherited from Zsum
GiNaC::ex	n

GiNaC::ex	letter_list

Detailed Description

A harmonic polylog is a special case of a multiple polylog.

Harmonic polylogs are defined by

$\mbox{H}_{m_1,...,m_k}(x) = \mbox{Li}_{m_k,...,m_1}(1,...,1,x)$

There are two "print" formats available. The default option prints harmonic polylogarithms as 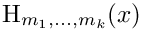$\mbox{H}_{m_1,...,m_k}(x)$ .

If the flag "print_format::no_harmonic_polylog" in the variable "_print_format" is set, harmonic polylogarithms are printed as multiple polylogarithms, e.g. in the 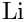$\mbox{Li}$ - notation.

Member Function Documentation

◆ eval()

ex eval ( ) const

override

The simplifications are done in the following order:

If all degrees are equal to 1 except the first one, we have a Nielsen polylog.

The documentation for this class was generated from the following files:

Public Member Functions

Additional Inherited Members

Detailed Description

Member Function Documentation

◆ eval()