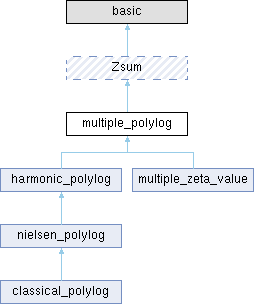
A multiple polylog sum is a special case of a Zsum. More...
#include <multiple_polylog.h>
Public Member Functions | |
| multiple_polylog (const GiNaC::ex &llc) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| GiNaC::ex | eval () const override |
| virtual GiNaC::ex | eval_approx () const |
 Public Member Functions inherited from Zsum Public Member Functions inherited from Zsum | |
| Zsum (const GiNaC::ex &nc) | |
| Zsum (const GiNaC::ex &nc, const GiNaC::ex &llc) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | convert_to_Ssum_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1) const |
| virtual GiNaC::ex | shuffle_exvector (const GiNaC::exvector &Z0, const GiNaC::exvector &Z1, const GiNaC::exvector &Z2) const |
| virtual GiNaC::ex | set_index (const GiNaC::ex &i) const |
| virtual GiNaC::ex | shift_plus_one (void) const |
| virtual GiNaC::ex | shift_minus_one (void) const |
| virtual GiNaC::ex | adjust_upper_limit_downwards (const GiNaC::ex &i) const |
| virtual GiNaC::ex | adjust_upper_limit_upwards (const GiNaC::ex &i) const |
| virtual GiNaC::ex | adjust_upper_limit_plus_one (void) const |
| virtual GiNaC::ex | index_eq_one (void) const |
| virtual GiNaC::ex | get_head (int k) const |
| virtual GiNaC::ex | get_tail (int k) const |
| virtual GiNaC::ex | antipode (void) const |
| virtual GiNaC::ex | expand_members (int level=0) const |
| virtual GiNaC::ex | eval_explicit () const |
| virtual GiNaC::ex | get_first_letter (void) const |
| virtual GiNaC::ex | remove_first_letter (void) const |
| virtual GiNaC::ex | remove_first_letter (const GiNaC::ex &nc) const |
| virtual GiNaC::ex | prepend_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | prepend_letter (const GiNaC::ex &nc, const GiNaC::ex &lc) const |
| virtual GiNaC::ex | append_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | append_letter_list (const GiNaC::ex &lc) const |
| GiNaC::ex | get_index (void) const |
| GiNaC::ex | get_letter_list (void) const |
| unsigned | get_depth (void) const |
| GiNaC::ex | get_weight (void) const |
Additional Inherited Members | |
 Protected Member Functions inherited from Zsum Protected Member Functions inherited from Zsum | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
| virtual GiNaC::ex | cast_to_Ssum (void) const |
| virtual GiNaC::ex | multiply_letter_with_last_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | multiply_letter_with_first_letter (const GiNaC::ex &lc) const |
| virtual GiNaC::ex | concat_two_sums (const GiNaC::ex &Z1, const GiNaC::ex &Z2) const |
 Protected Attributes inherited from Zsum Protected Attributes inherited from Zsum | |
| GiNaC::ex | n |
| GiNaC::ex | letter_list |
Detailed Description
A multiple polylog sum is a special case of a Zsum.
Multiple polylogs are in the notation of Goncharov defined by
![\[
\mbox{Li}_{m_k,...,m_1}(x_k,...,x_1) = Z(\infty;m_1,...,m_k;x_1,...,x_k)
\]](form_122.png)
There are two "print" formats available. The default option prints multiple polylogarithms with reversed order of the arguments, as in the definition above. This notation is for example used by Goncharov.
If the flag "print_format::no_reversed_order" in the variable "_print_format" is set, multiple polylogarithms are printed without reversing the order of the arguments, e.g.
![\[
Z(\infty;m_1,...,m_k;x_1,...,x_k) = \mbox{Li}_{m_1,...,m_k}(x_1,...,x_k)
\]](form_123.png)
This notation is used in the french literature.
Member Function Documentation
◆ eval()
|
override |
The simplifications are done in the following order:
- If all
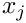
- If all
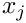
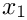
◆ eval_approx()
|
virtual |
This method provides a simple numerical evaluation routine for multiple polylogarithms.
Multiple polylogarithms are evaluated as power series up to an upper summation limit _NMAX.
This is not a routine designed for performance. It only provides a simple way to check a result for a few selected points.
The documentation for this class was generated from the following files:
Generated by