root_of_unity Class Reference
#include <root_of_unity.h>
Inheritance diagram for root_of_unity:
Public Member Functions | |
| root_of_unity (unsigned l, unsigned k) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
Protected Member Functions | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
Protected Attributes | |
| unsigned | l |
| unsigned | k |
Detailed Description
A root of unity is defined by
![\[
r_k^l = \exp \left( \frac{2 \pi i l}{k} \right)
\]](form_166.png)
Member Function Documentation
◆ eval()
|
override |
The following simplifications are done:
- If
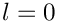
- If
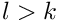
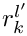
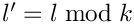
- If
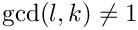
◆ eval_ncmul()
|
overrideprotected |
Multiplication is done according to
![\[
r_{k_1}^{l_1} r_{k_2}^{l_2} = \exp \left( 2 \pi i \frac{k_2 l_1 + k_1 l_2}{k_1 k_2} \right)
\]](form_165.png)
The documentation for this class was generated from the following files:
Generated by