#include <transc_fct_C.h>

Inheritance diagram for transcendental_fct_type_C:

Public Member Functions
	transcendental_fct_type_C (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom)

	transcendental_fct_type_C (const GiNaC::ex &xx1, const GiNaC::ex &xx2, const GiNaC::ex &ii_num, const GiNaC::ex &ii_denom, const GiNaC::ex &iijj_num, const GiNaC::ex &iijj_denom, const GiNaC::ex &pp_num, const GiNaC::ex &pp_denom, const GiNaC::ex &eps, int o, int f)

void	archive (GiNaC::archive_node &node) const override

void	read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override

unsigned	return_type (void) const override

void	print (const GiNaC::print_context &c, unsigned level=0) const override

unsigned	precedence (void) const override

GiNaC::ex	eval () const override

GiNaC::ex	subs (const GiNaC::exmap &m, unsigned options=0) const override

GiNaC::ex	set_expansion (const GiNaC::ex &eps, int o) const

GiNaC::ex	shift_plus_one (void) const

Protected Member Functions
GiNaC::ex	eval_ncmul (const GiNaC::exvector &v) const override

GiNaC::ex	derivative (const GiNaC::symbol &s) const override

unsigned	calchash (void) const override

Protected Attributes
GiNaC::ex	x1

GiNaC::ex	x2

GiNaC::ex	i_num

GiNaC::ex	i_denom

GiNaC::ex	ij_num

GiNaC::ex	ij_denom

GiNaC::ex	pre_num

GiNaC::ex	pre_denom

GiNaC::ex	expansion_parameter

int	order

int	flag_expand_status

Detailed Description

The class transcendental_fct_type_C provides an interface to the class transcendental_sum_type_C. The definition is

$\frac{\Gamma(d_1) ... \Gamma(d_n)}{\Gamma(d_1') ... \Gamma(d_{n'}')} \sum\limits_{i=0}^\infty \sum\limits_{j=0}^\infty \frac{\Gamma(i+a_1) ... \Gamma(i+a_k)}{\Gamma(i+a_1') ... \Gamma(i+a_{k}')} \frac{\Gamma(i+j+c_1) ... \Gamma(i+j+c_m)}{\Gamma(i+j+c_1') ... \Gamma(i+j+c_{m-1}')} \frac{x_1^i}{i!} \frac{x_2^j}{j!}$

Member Function Documentation

◆ eval()

ex eval ( ) const

override

Evaluation: If flag_expand_status is set, the object is expanded in 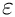$\varepsilon$ .

The result is converted to a standard form, using convert_Zsums_to_standard_form.

◆ eval_ncmul()

ex eval_ncmul ( const GiNaC::exvector & v ) const

overrideprotected

No automatic simplifications

◆ set_expansion()

ex set_expansion	(	const GiNaC::ex &	eps,
		int	o ) const

Sets the flag flag_expand_status to expand_status::expansion_required. The object is then automatically expanded up to the specified order.

◆ shift_plus_one()

ex shift_plus_one ( void ) const

Casts a sum of the form

$\frac{\Gamma(d_1) ... \Gamma(d_n)}{\Gamma(d_1') ... \Gamma(d_{n'}')} \sum\limits_{i=1}^\infty \sum\limits_{j=0}^\infty \frac{\Gamma(i+a_1) ... \Gamma(i+a_k)}{\Gamma(i+a_1') ... \Gamma(i+a_{k}')} \frac{\Gamma(i+j+c_1) ... \Gamma(i+j+c_m)}{\Gamma(i+j+c_1') ... \Gamma(i+j+c_{m-1}')} \frac{x_1^i}{i!} \frac{x_2^j}{j!}$

into the form of transcendental_fct_type_C by making the change of variables

$i' = i-1$

The documentation for this class was generated from the following files:

Public Member Functions