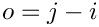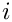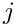The class list_of_tgamma is a container for the class ratio_of_tgamma. More...
#include <list_polygamma.h>
Public Member Functions | |
| list_of_tgamma (const GiNaC::ex &l) | |
| list_of_tgamma (const GiNaC::ex &l, const GiNaC::ex &i, const GiNaC::ex &eps, int o) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | eval_explicit () const |
| virtual unsigned | get_key (void) const |
| virtual GiNaC::ex | hash_data (void) const |
| virtual GiNaC::ex | subst_data (void) const |
| GiNaC::ex | set_expansion (void) const |
| GiNaC::ex | set_index (const GiNaC::ex &new_index) const |
| GiNaC::ex | set_expansion_parameter (const GiNaC::ex &new_eps) const |
| GiNaC::ex | set_order (int new_order) const |
| GiNaC::ex | get_index (void) const |
| unsigned | get_depth (void) const |
| GiNaC::ex | shift_plus_one (void) const |
| GiNaC::ex | shift_minus_one (void) const |
| GiNaC::ex | index_eq_one (void) const |
| GiNaC::ex | shift_index (const GiNaC::ex &new_index) const |
| GiNaC::ex | concat (const GiNaC::ex &l) const |
| int | pole_alert (void) const |
| int | expansion_alert (void) const |
Protected Member Functions | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
Protected Attributes | |
| GiNaC::ex | gamma_sequence |
| GiNaC::ex | index |
| GiNaC::ex | expansion_parameter |
| int | order |
Friends | |
| class | transcendental_sum_type_A |
| class | transcendental_sum_type_B |
| class | transcendental_sum_type_C |
| class | transcendental_sum_type_D |
| GiNaC::ex | create_transcendental_sum_type_A_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_B_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_C_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &v, const GiNaC::ex &ss, const GiNaC::ex &eps, int o, int f) |
| GiNaC::ex | create_transcendental_sum_type_D_and_set_gammas (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) |
Detailed Description
Member Function Documentation
◆ concat()
| ex concat | ( | const GiNaC::ex & | l | ) | const |
Concats two list_of_tgammas.
◆ eval()
|
override |
If the index is an integer, the object is evaluated explicitly.
◆ eval_explicit()
|
virtual |
Explicit evaluation. The job is delegated to the function nestedsums_helper_expand_lst_tgamma_fct.
◆ eval_ncmul()
|
overrideprotected |
If two list_of_tgammas have the same index, they can be merged together.
If the difference between the two indices is an integer, we can merge them according to
![\[
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(1+d_2\varepsilon)}{\Gamma(1+b_2\varepsilon)}
\frac{\Gamma((i+l)+a_1+b_1 \varepsilon)}{\Gamma((i+l)+c_1+d_1 \varepsilon)}
\frac{\Gamma(i+a_2+b_2 \varepsilon)}{\Gamma(i+c_2+d_2 \varepsilon)}
\]](form_105.png)
![\[
=
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(1+d_2\varepsilon)}{\Gamma(1+b_2\varepsilon)}
\frac{\Gamma(i+(a_1+l)+b_1 \varepsilon)}{\Gamma(i+(c_1+l)+d_1 \varepsilon)}
\frac{\Gamma(i+a_2+b_2 \varepsilon)}{\Gamma(i+c_2+d_2 \varepsilon)}
\]](form_106.png)
where 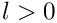
◆ expansion_alert()
| int expansion_alert | ( | void | ) | const |
Returns 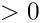
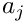
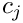
◆ get_depth()
|
inline |
Returns the depth.
◆ get_index()
|
inline |
Returns the upper summation limit.
◆ get_key()
|
virtual |
Returns the hash key to be used in connection with the class hash_entry.
◆ hash_data()
|
virtual |
Returns an expression which allows a comparison up to equivalence with an entry in a hash map.
In this case the comparison is exact and the method returns *this.
◆ index_eq_one()
| ex index_eq_one | ( | void | ) | const |
Returns
![\[
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)} ...
\frac{\Gamma(1+d_k\varepsilon)}{\Gamma(1+b_k\varepsilon)}
\frac{\Gamma(a_1+1+b_1 \varepsilon)}{\Gamma(c_1+1+d_1 \varepsilon)} ...
\frac{\Gamma(a_k+1+b_k \varepsilon)}{\Gamma(c_k+1+d_k \varepsilon)}
\]](form_110.png)
◆ pole_alert()
| int pole_alert | ( | void | ) | const |
Returns 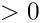
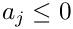
◆ set_expansion()
| ex set_expansion | ( | void | ) | const |
Sets the flag expansion_required for ratio_of_tgamma. The object is then automatically expanded up to the order specified in the member variable order.
This function should be called after all possible poles have been taken care of, e.g. all 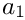
The result is in expanded form.
◆ set_expansion_parameter()
| ex set_expansion_parameter | ( | const GiNaC::ex & | new_eps | ) | const |
Sets the member variable expansion_parameter to new_eps.
◆ set_index()
| ex set_index | ( | const GiNaC::ex & | new_index | ) | const |
Sets the member variable index to new_index.
◆ set_order()
| ex set_order | ( | int | new_order | ) | const |
Sets the member variable order to new_order.
◆ shift_index()
| ex shift_index | ( | const GiNaC::ex & | new_index | ) | const |
◆ shift_minus_one()
| ex shift_minus_one | ( | void | ) | const |
Returns
![\[
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)} ...
\frac{\Gamma(1+d_k\varepsilon)}{\Gamma(1+b_k\varepsilon)}
\frac{\Gamma(i+a_1-1+b_1 \varepsilon)}{\Gamma(i+c_1-1+d_1 \varepsilon)} ...
\frac{\Gamma(i+a_k-1+b_k \varepsilon)}{\Gamma(i+c_k-1+d_k \varepsilon)}
\]](form_109.png)
The order parameter is not changed.
◆ shift_plus_one()
| ex shift_plus_one | ( | void | ) | const |
Returns
![\[
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)} ...
\frac{\Gamma(1+d_k\varepsilon)}{\Gamma(1+b_k\varepsilon)}
\frac{\Gamma(i+a_1+1+b_1 \varepsilon)}{\Gamma(i+c_1+1+d_1 \varepsilon)} ...
\frac{\Gamma(i+a_k+1+b_k \varepsilon)}{\Gamma(i+c_k+1+d_k \varepsilon)}
\]](form_108.png)
The order parameter is not changed.
◆ subst_data()
|
virtual |
Returns the data which has to be substitued if the comparison with a hash entry is only up to equivalence.
In this case, the comparison is exact, and no data needs to be substituted.
Friends And Related Symbol Documentation
◆ create_transcendental_sum_type_A_and_set_gammas
|
friend |
Named ctor on the heap.
◆ create_transcendental_sum_type_B_and_set_gammas
|
friend |
Named ctor on the heap.
◆ create_transcendental_sum_type_C_and_set_gammas
|
friend |
Named ctor on the heap.
◆ create_transcendental_sum_type_D_and_set_gammas
|
friend |
Named ctor on the heap.
The documentation for this class was generated from the following files:
Generated by
![\[
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(1+d_2\varepsilon)}{\Gamma(1+b_2\varepsilon)} ...
\frac{\Gamma(1+d_k\varepsilon)}{\Gamma(1+b_k\varepsilon)}
\]](form_118.png)
![\[
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)}
\frac{\Gamma(i+a_2+b_2\varepsilon)}{\Gamma(i+c_2+d_2\varepsilon)} ...
\frac{\Gamma(i+a_k+b_k\varepsilon)}{\Gamma(i+c_k+d_k\varepsilon)}
\]](form_119.png)
![\[
\Gamma(i + a + o + b \varepsilon )
\]](form_111.png)