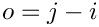The class ratio_of_tgamma contains the ratio of two Gamma functions. More...
#include <polygamma.h>
Public Member Functions | |
| ratio_of_tgamma (const GiNaC::ex &a1, const GiNaC::ex &b1, const GiNaC::ex &a2, const GiNaC::ex &b2) | |
| ratio_of_tgamma (const GiNaC::ex &a1, const GiNaC::ex &b1, const GiNaC::ex &a2, const GiNaC::ex &b2, const GiNaC::ex &i, const GiNaC::ex &eps, int o, int f) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | eval_explicit () const |
| GiNaC::ex | set_expansion (void) const |
| GiNaC::ex | set_index (const GiNaC::ex &new_index) const |
| GiNaC::ex | set_expansion_parameter (const GiNaC::ex &new_eps) const |
| GiNaC::ex | set_order (int new_order) const |
| GiNaC::ex | set_flag (int new_flag) const |
| GiNaC::ex | set_values (const GiNaC::ex &new_index, const GiNaC::ex &new_eps, int new_order, int new_flag) const |
| GiNaC::ex | get_index (void) const |
| GiNaC::ex | shift_plus_one (void) const |
| GiNaC::ex | shift_minus_one (void) const |
| GiNaC::ex | index_eq_one (void) const |
| GiNaC::ex | shift_index (const GiNaC::ex &new_index) const |
| int | pole_alert (void) const |
| int | expansion_alert (void) const |
Protected Member Functions | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
| GiNaC::ex | increase_numerator (int shift_order=0) const |
| GiNaC::ex | decrease_numerator (int shift_order=0) const |
| GiNaC::ex | increase_denominator (int shift_order=0) const |
| GiNaC::ex | decrease_denominator (int shift_order=0) const |
| GiNaC::ex | prefactor_increase_numerator (void) const |
| GiNaC::ex | prefactor_decrease_numerator (void) const |
| GiNaC::ex | prefactor_increase_denominator (void) const |
| GiNaC::ex | prefactor_decrease_denominator (void) const |
Protected Attributes | |
| GiNaC::ex | a1 |
| GiNaC::ex | b1 |
| GiNaC::ex | a2 |
| GiNaC::ex | b2 |
| GiNaC::ex | index |
| GiNaC::ex | expansion_parameter |
| int | order |
| int | flag_expand_status |
Friends | |
| class | list_of_tgamma |
Detailed Description
The class ratio_of_tgamma contains the ratio of two Gamma functions.
The definition is
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
\]](form_154.png)
Here 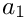
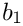
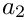

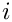
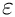
Additionally, this class contains an internal variable "order", which indicates to which order this object should be expanded. The "order" variable can be set via the method set_order(int). The expansion is performed by calling the method set_expansion(void).
This class assumes that 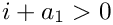
Member Function Documentation
◆ decrease_denominator()
|
protected |
Returns
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2-1+b_2\varepsilon)}
\]](form_145.png)
The order variable is adjusted according to order = order + shift_order.
◆ decrease_numerator()
|
protected |
Returns
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1-1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
\]](form_143.png)
The order variable is adjusted according to order = order + shift_order.
◆ eval()
|
override |
If the flag flag_expand_status is set, the object is expanded in 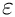
If 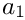
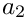
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+b_1\varepsilon)}{\Gamma(i+b_2\varepsilon)}
= \frac{ 1 + b_1 \varepsilon Z_1(i-1) + ...}{1 + b_2 \varepsilon Z_1(i-1) + ...}
\]](form_129.png)
Here the formula
![\[
\left( 1 + \varepsilon Z_1(i-1) + \varepsilon^2 Z_{11}(i-1) + ... \right)^{-1}
= 1 - \varepsilon S_1(i-1) + \varepsilon^2 S_{11}(i-1) - ...
\]](form_130.png)
is useful.
If 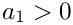
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
= \left( i + a_1 -1 + b_1 \varepsilon \right)
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1-1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
\]](form_132.png)
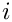
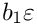
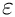
If 
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
= \sum\limits_{j=0}^\infty \frac{1}{(i+a_1)^{j+1}} \left(-b_1\right)^j \varepsilon^j
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
\]](form_135.png)
The order parameter is adjusted according to the prefactors of 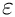
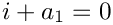
If 
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
= \sum\limits_{j=0}^\infty \frac{1}{(i+a_2-1)^{j+1}} \left(-b_2\right)^j \varepsilon^j
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2-1+b_2\varepsilon)}
\]](form_138.png)
The order parameter is adjusted according to the prefactors of 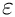
If 
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
= \left( i + a_2 + b_2 \varepsilon \right)
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+1+b_2\varepsilon)}
\]](form_140.png)
The order parameter is adjusted according to the prefactors of 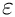
The return type is either Zsum or basic_letter * Zsum. If 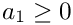
If the index is an integer and the status flag not equal to no_eval_to_scalar, the object is evaluated explicitly.
◆ eval_explicit()
|
virtual |
Explicit evaluation with the help of nestedsums_helper_expand_tgamma_fct.
◆ eval_ncmul()
|
overrideprotected |
No automatic simplifications
◆ expansion_alert()
| int expansion_alert | ( | void | ) | const |
Returns 1 if 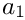
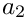
◆ get_index()
| ex get_index | ( | void | ) | const |
Returns the index.
◆ increase_denominator()
|
protected |
Returns
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+a_2+1+b_2\varepsilon)}
\]](form_144.png)
The order variable is adjusted according to order = order + shift_order.
◆ increase_numerator()
|
protected |
Returns
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+1+b_1\varepsilon)}{\Gamma(i+a_2+b_2\varepsilon)}
\]](form_142.png)
The order variable is adjusted according to order = order + shift_order.
◆ index_eq_one()
| ex index_eq_one | ( | void | ) | const |
Returns the expansions of
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(a_1+1+b_1 \varepsilon)}{\Gamma(a_2+1+b_2 \varepsilon)}
\]](form_152.png)
up to order + shift_order.
◆ pole_alert()
| int pole_alert | ( | void | ) | const |
Returns 1 if 
◆ prefactor_decrease_denominator()
|
protected |
Returns
![\[
\sum\limits_{j=0}^\infty \frac{1}{(i+a_2-1)^{j+1}} \left(-b_2\right)^j \varepsilon^j
\]](form_149.png)
◆ prefactor_decrease_numerator()
|
protected |
Returns
![\[
\left(i + a_1-1 \right) +b_1 \varepsilon i^0
\]](form_147.png)
◆ prefactor_increase_denominator()
|
protected |
Returns
![\[
i + a_2 i^0 + b_2 \varepsilon i^0
\]](form_148.png)
◆ prefactor_increase_numerator()
|
protected |
Returns
![\[
\sum\limits_{j=0}^\infty \frac{1}{(i+a_1)^{j+1}} \left(-b_1\right)^j \varepsilon^j
\]](form_146.png)
◆ set_expansion()
| ex set_expansion | ( | void | ) | const |
Sets the flag expansion_required. The object is then automatically expanded up to the order specified in the member variable order.
◆ set_expansion_parameter()
| ex set_expansion_parameter | ( | const GiNaC::ex & | new_eps | ) | const |
Sets the member variable expansion_parameter to new_eps.
◆ set_flag()
| ex set_flag | ( | int | new_flag | ) | const |
Sets the member variable flag_expand_status to new_flag
◆ set_index()
| ex set_index | ( | const GiNaC::ex & | new_index | ) | const |
Sets the member variable index to new_index.
◆ set_order()
| ex set_order | ( | int | new_order | ) | const |
Sets the member variable order to new_order.
◆ set_values()
| ex set_values | ( | const GiNaC::ex & | new_index, |
| const GiNaC::ex & | new_eps, | ||
| int | new_order, | ||
| int | new_flag ) const |
Sets the member variables index, expansion_parameter and order to new values.
◆ shift_index()
| ex shift_index | ( | const GiNaC::ex & | new_index | ) | const |
◆ shift_minus_one()
| ex shift_minus_one | ( | void | ) | const |
Returns
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1-1+b_1 \varepsilon)}{\Gamma(i+a_2-1+b_2 \varepsilon)}
\]](form_151.png)
The order parameter is not changed.
◆ shift_plus_one()
| ex shift_plus_one | ( | void | ) | const |
Returns
![\[
\frac{\Gamma(1+b_2\varepsilon)}{\Gamma(1+b_1\varepsilon)}
\frac{\Gamma(i+a_1+1+b_1 \varepsilon)}{\Gamma(i+a_2+1+b_2 \varepsilon)}
\]](form_150.png)
The order parameter is not changed.
The documentation for this class was generated from the following files:
Generated by
![\[
\Gamma(i + a + o + b \varepsilon )
\]](form_111.png)