Nestedsums library
Public Member Functions | Protected Member Functions | Protected Attributes | List of all members
transcendental_sum_type_B Class Reference

The class transcendental_sum_type_B may contain 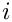$i$ and $(n-i)$. More...

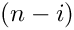
#include <transcendental_B.h>

Inheritance diagram for transcendental_sum_type_B:

Public Member Functions

 transcendental_sum_type_B (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f)
 
void archive (GiNaC::archive_node &node) const override
 
void read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override
 
unsigned return_type (void) const override
 
void print (const GiNaC::print_context &c, unsigned level=0) const override
 
unsigned precedence (void) const override
 
GiNaC::ex eval () const override
 
GiNaC::ex subs (const GiNaC::exmap &m, unsigned options=0) const override
 
virtual GiNaC::ex eval_explicit () const
 
GiNaC::ex set_expansion (void) const
 
GiNaC::ex distribute_over_subsum (void) const
 
GiNaC::ex distribute_over_letter (void) const
 
GiNaC::ex distribute_over_subsum_rev (void) const
 
GiNaC::ex distribute_over_letter_rev (void) const
 
GiNaC::ex shift_plus_one (void) const
 
GiNaC::ex shift_plus_one_rev (void) const
 

Protected Member Functions

GiNaC::ex eval_ncmul (const GiNaC::exvector &v) const override
 
GiNaC::ex derivative (const GiNaC::symbol &s) const override
 
unsigned calchash (void) const override
 

Protected Attributes

GiNaC::ex n
 
GiNaC::ex index
 
GiNaC::ex letter
 
GiNaC::ex letter_rev
 
GiNaC::ex lst_of_gammas
 
GiNaC::ex lst_of_gammas_rev
 
GiNaC::ex subsum
 
GiNaC::ex subsum_rev
 
GiNaC::ex expansion_parameter
 
int order
 
int flag_expand_status
 

Detailed Description

The class transcendental_sum_type_B may contain $i$ and $(n-i)$.

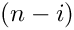
The definition is

\[ \frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)} ... \frac{\Gamma(1+d_k\varepsilon)}{\Gamma(1+b_k\varepsilon)} \frac{\Gamma(1+d_1'\varepsilon)}{\Gamma(1+b_1'\varepsilon)} ... \frac{\Gamma(1+d_{k'}'\varepsilon)}{\Gamma(1+b_{k'}'\varepsilon)} \]

\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} \frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} \frac{\Gamma(i+a_2+b_2\varepsilon)}{\Gamma(i+c_2+d_2\varepsilon)} ... \frac{\Gamma(i+a_k+b_k\varepsilon)}{\Gamma(i+c_k+d_k\varepsilon)} Z(i+o-1,m_1,...,m_l,x_1,...,x_l) \]

\[ \cdot \frac{y^{n-i}}{(n-i+c')^{m'}} \frac{\Gamma(n-i+a_1'+b_1'\varepsilon)}{\Gamma(n-i+c_1'+d_1'\varepsilon)} \frac{\Gamma(n-i+a_2'+b_2'\varepsilon)}{\Gamma(n-i+c_2'+d_2'\varepsilon)} ... \frac{\Gamma(n-i+a_{k'}'+b_{k'}'\varepsilon)}{\Gamma(n-i+c_{k'}'+d_{k'}'\varepsilon)} Z(n-i+o'-1,m_1',...,m_{l'}',x_1',...,x_{l'}') \]

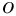
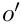
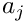
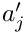
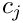
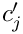
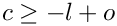
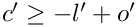
Here, $c$, $c'$, $o$, $o'$ and all $a_j$, $a_j'$, $c_j$ and $c_j'$ are integers. In addition $c$ is non-negative or $ c \ge -l+o $. Simmilar, $c'$ is non-negative or $ c' \ge -l'+o' $.

Note that the upper summation limit is 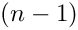$(n-1)$. The upper summation limit should not be infinity.

Member Function Documentation

◆ distribute_over_letter()

ex distribute_over_letter ( void ) const

letter is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars and basic_letters.

This routine converts the transcendental_sum_type_B to a canonical form, so that afterwards letter only contains a basic_letter.

◆ distribute_over_letter_rev()

ex distribute_over_letter_rev ( void ) const

letter_rev is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars and basic_letters.

This routine converts the transcendental_sum_type_B to a canonical form, so that afterwards letter_rev only contains a basic_letter.

◆ distribute_over_subsum()

ex distribute_over_subsum ( void ) const

subsum is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars, basic_letters, list_of_tgammas, Zsums or Ssums.

This routine converts the transcendental_sum_type_B to a canonical form, so that afterwards subsum only contains a Zsum.

The algorithm is based on the following steps:

  • If an object is of type basic_letter and the difference of its index with the index member is an integer, it is combined with the letter member. Otherwise it is taken out of the sum.
  • If an object is of type list_of_tgamma and the difference of its index with the index member is an integer, it is combined with the lst_of_gammas member. Otherwise it is taken out of the sum.
  • If an object is of type Zsum and the difference of its index with the index member is an integer, it is stays inside the subsum. Otherwise it is taken out of the sum.
  • If an object is of type Ssum and the difference of its index with the index member is an integer, it is converted to an Zsum and stays inside the subsum. Otherwise it is taken out of the sum.

◆ distribute_over_subsum_rev()

ex distribute_over_subsum_rev ( void ) const

subsum_rev is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars, basic_letters, list_of_tgammas, Zsums or Ssums.

This routine converts the transcendental_sum_type_B to a canonical form, so that afterwards subsum_rev only contains a Zsum.

The algorithm is based on the following steps:

  • If an object is of type basic_letter and the difference of its index with $(n-i)$ is an integer, it is combined with the letter_rev member. Otherwise it is taken out of the sum.
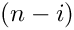
  • If an object is of type list_of_tgamma and the difference of its index with $(n-i)$ is an integer, it is combined with the lst_of_gammas_rev member. Otherwise it is taken out of the sum.
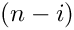
  • If an object is of type Zsum and the difference of its index with $(n-i)$ is an integer, it is stays inside the subsum_rev. Otherwise it is taken out of the sum.
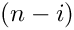
  • If an object is of type Ssum and the difference of its index with $(n-i)$ is an integer, it is converted to an Zsum and stays inside the subsum_rev. Otherwise it is taken out of the sum.

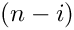
◆ eval()

ex eval ( ) const
override

Simplifications, which are always performed are:

  • If subsum is equal to 1, the subsum is replaced with Z(i-1).
  • If subsum_rev is equal to 1, the subsum_rev is replaced with Z(n-i-1).
  • If subsum is not of type Zsum, the routine distribute_over_subsum is called.
  • If the difference of the upper summation index of the Zsum (in subsum) with the index member is not an integer, the Zsum is taken out of the sum. The subsum is replaced with Z(i-1).
  • If subsum_rev is not of type Zsum, the routine distribute_over_subsum_rev is called.
  • If the difference of the upper summation index of the Zsum (in subsum_rev) with $(n-i)$ is not an integer, the Zsum is taken out of the sum. The subsum_rev is replaced with Z(n-i-1).
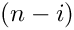
  • If letter is not of type basic_letter, the routine distribute_over_letter is called.
  • If the difference of the index of the basic_letter (in letter) with the index member is not zero, the index in basic_letter is adjusted.
  • If letter_rev is not of type basic_letter, the routine distribute_over_letter_rev is called.
  • If the difference of the index of the basic_letter (in letter_rev) with $(n-i)$ is not zero, the index in basic_letter is adjusted.
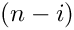
  • If the difference of the index of lst_of_gammas with the index member is not zero, the index in lst_of_gammas is adjusted.
  • If the difference of the index of lst_of_gammas_rev with $(n-i)$ is not zero, the index in lst_of_gammas_rev is adjusted.

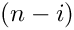
If flag_expand_status == expand_status::expansion_required, the evaluation routine performs a set of consistency checks:

  • It adjusts the upper summation limit to index-1 in subsum and to n-index-1 in subsum_rev. If $ o > 0 $ the function Zsum::adjust_upper_limit_downwards(index-1) is used. If $ o < 0 $ the function shift_plus_one() is called. If $ o' > 0 $ the function Zsum::adjust_upper_limit_downwards(n-index-1) is used. If $ o' < 0 $ the function shift_plus_one_rev() is called.
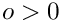
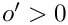
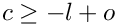
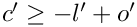
  • It checks, that letter and letter_rev do not give rise to poles (e.g. that the offset $c$ is a non-negative integer or a negative integer larger or equal to $c \ge -l+o $ and that the offset $c'$ is a non-negative integer or a negative integer larger or equal to $c' \ge -l'+o' $).
  • It checks, that the $a_j$ in the Gamma functions are integers.

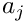
If one of the tests fails, the object is put into a zombie state.

If flag_expand_status == expand_status::check_for_poles, it assures that the Gamma functions in the numerator do not give rise to poles. The functions shift_plus_one() and shift_plus_one_rev() are used.

If flag_expand_status == expand_status::expand_gamma_functions, the Gamma functions are expanded into Euler Zagier sums. This is done by setting the expansion_required flag in the ratio_of_tgamma class.

If flag_expand_status == expand_status::do_partial_fractioning, the sum is of the form

\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} Z(i-1,m_1,...) \frac{y^{n-i}}{(n-i+c')^{m'}} Z(n-i-1,m_1',....) \]

For $m=0$ we have

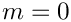
\[ x^n \sum\limits_{i=1}^{n-1} \frac{\left(\frac{y}{x}\right)^i}{(i+c')^{m'}} Z(i-1,m_1',...) Z(n-i-1,m_1,...) \]

For $m'=0$ we have

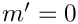
\[ y^n \sum\limits_{i=1}^{n-1} \frac{\left(\frac{x}{y}\right)^i}{(i+c)^{m}} Z(i-1,m_1,...) Z(n-i-1,m_1',...) \]

For $m'<0$ we use

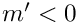
\[ (n-i+c') = (n+c') - i \]

For $m<0$ we use

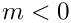
\[ (i+c) = (n+c) - (n-i) \]

For $m>0$ and $m'>0$ we have

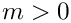
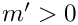
\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} Z(i-1,m_1,...) \frac{y^{n-i}}{(n-i+c')^{m'}} Z(n-i-1,m_1',....) \]

\[ = \frac{1}{n+c+c'} \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^{m-1}} Z(i-1,...) \frac{y^{n-i}}{(n-i+c')^{m'}} Z(n-i-1,....) \]

\[ \mbox{} + \frac{1}{n+c+c'} \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^{m}} Z(i-1,...) \frac{y^{n-i}}{(n-i+c')^{m'-1}} Z(n-i-1,....) \]

If flag_expand_status == expand_status::do_outermost_sum, the sum is of the form

\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} Z(i-1,m_1,...) Z(n-i-1,m_1',....) \]

If the depth of 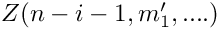$Z(n-i-1,m_1',....)$ is zero, we have a sum of type A with upper summation index $(n-1)$:

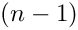
\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} Z(i-1,m_1,...) \]

Otherwise we have the recursion

\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} Z(i-1,m_1,...) Z(n-i-1,m_1',....) \]

\[ = \sum\limits_{j=1}^{n-1} \left[ \sum\limits_{i=1}^{j-1} \frac{x^i}{(i+c)^m} Z(i-1,m_1,...) \frac{{x_1'}^{j-i}}{(j-i)^{m_1'}} Z(j-i-1,m_2',....) \right] \]

◆ eval_explicit()

ex eval_explicit ( ) const
virtual

Explicit evaluation

◆ eval_ncmul()

ex eval_ncmul ( const GiNaC::exvector & v) const
overrideprotected

No automatic simplifications

◆ set_expansion()

ex set_expansion ( void ) const

Sets the flag flag_expand_status to expand_status::expansion_required. The object is then automatically expanded up to the order specified in the member variable order.

◆ shift_plus_one()

ex shift_plus_one ( void ) const

This routine performs the substitution index -> index - 1. The formula used is

\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} \frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} ... Z(i-1+o,m_1,...,m_l,x_1,...,x_l) \cdot \frac{y^{n-i}}{(n-i+c')^{m'}} \frac{\Gamma(n-i+a_1'+b_1'\varepsilon)}{\Gamma(n-i+c_1'+d_1'\varepsilon)} ... Z(n-i-1+o',m_1',...,m_{l'}',x_1',...,x_{l'}') \]

\[ = x \sum\limits_{i=1}^{n-2} \frac{x^i}{(i+c+1)^m} \frac{\Gamma(i+a_1+1+b_1\varepsilon)}{\Gamma(i+c_1+1+d_1\varepsilon)} ... Z(i+o,m_1,...,m_l,x_1,...,x_l) \cdot \frac{y^{n-1-i}}{(n-1-i+c')^{m'}} \frac{\Gamma(n-1-i+a_1'+b_1'\varepsilon)}{\Gamma(n-1-i+c_1'+d_1'\varepsilon)} ... Z(n-1-i-1+o',m_1',...,m_{l'}',x_1',...,x_{l'}') \]

\[ + \frac{x}{(c+1)^m} \frac{\Gamma(a_1+1+b_1\varepsilon)}{\Gamma(c_1+1+d_1\varepsilon)} ... Z(o,m_1,...,m_l,x_1,...,x_l) \cdot \frac{y^{n-1}}{(n-1+c')^{m'}} \frac{\Gamma(n-1+a_1'+b_1'\varepsilon)}{\Gamma(n-1+c_1'+d_1'\varepsilon)} ... Z(n-2+o',m_1',...,m_{l'}',x_1',...,x_{l'}') Z(n-2) \]

This routine is called from eval/expansion_required, and eval/check_for_poles.

◆ shift_plus_one_rev()

ex shift_plus_one_rev ( void ) const

This routine takes out the term at index = n - 1. The formula used is

\[ \sum\limits_{i=1}^{n-1} \frac{x^i}{(i+c)^m} \frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} ... Z(i-1+o,m_1,...,m_l,x_1,...,x_l) \cdot \frac{y^{n-i}}{(n-i+c')^{m'}} \frac{\Gamma(n-i+a_1'+b_1'\varepsilon)}{\Gamma(n-i+c_1'+d_1'\varepsilon)} ... Z(n-i-1+o',m_1',...,m_{l'}',x_1',...,x_{l'}') \]

\[ = y \sum\limits_{i=1}^{n-2} \frac{x^i}{(i+c)^m} \frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} ... Z(i-1+o,m_1,...,m_l,x_1,...,x_l) \cdot \frac{y^{n-1-i}}{(n-1-i+c'+1)^{m'}} \frac{\Gamma(n-1-i+a_1'+1+b_1'\varepsilon)}{\Gamma(n-1-i+c_1'+1+d_1'\varepsilon)} ... Z(n-1-i+o',m_1',...,m_{l'}',x_1',...,x_{l'}') \]

\[ + \frac{x^{n-1}}{(n-1+c)^m} \frac{\Gamma(n-1+a_1+b_1\varepsilon)}{\Gamma(n-1+c_1+d_1\varepsilon)} ... Z(n-2+o,m_1,...,m_l,x_1,...,x_l) \cdot \frac{y}{(1+c')^{m'}} \frac{\Gamma(a_1'+1+b_1'\varepsilon)}{\Gamma(c_1'+1+d_1'\varepsilon)} ... Z(o',m_1',...,m_{l'}',x_1',...,x_{l'}') Z(n-2) \]

This routine is called from eval/expansion_required, and eval/check_for_poles.

The documentation for this class was generated from the following files:
Generated by doxygen 1.12.0