#include <transcendental_D.h>

Public Member Functions | |
| transcendental_sum_type_D (const GiNaC::ex &nn, const GiNaC::ex &i, const GiNaC::ex &l, const GiNaC::ex &lr, const GiNaC::ex &v, const GiNaC::ex &vr, const GiNaC::ex &ss, const GiNaC::ex &ssr, const GiNaC::ex &eps, int o, int f) | |
| void | archive (GiNaC::archive_node &node) const override |
| void | read_archive (const GiNaC::archive_node &node, GiNaC::lst &sym_lst) override |
| unsigned | return_type (void) const override |
| void | print (const GiNaC::print_context &c, unsigned level=0) const override |
| unsigned | precedence (void) const override |
| GiNaC::ex | eval () const override |
| GiNaC::ex | subs (const GiNaC::exmap &m, unsigned options=0) const override |
| virtual GiNaC::ex | eval_explicit () const |
| GiNaC::ex | set_expansion (void) const |
| GiNaC::ex | distribute_over_subsum (void) const |
| GiNaC::ex | distribute_over_letter (void) const |
| GiNaC::ex | distribute_over_subsum_rev (void) const |
| GiNaC::ex | distribute_over_letter_rev (void) const |
| GiNaC::ex | shift_plus_one (void) const |
| GiNaC::ex | shift_plus_one_rev (void) const |
| GiNaC::ex | shift_minus_one (void) const |
Protected Member Functions | |
| GiNaC::ex | eval_ncmul (const GiNaC::exvector &v) const override |
| GiNaC::ex | derivative (const GiNaC::symbol &s) const override |
| unsigned | calchash (void) const override |
Detailed Description
The class transcendental_sum_type_D involves a conjugation and may contain 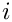
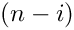
![\[
\frac{\Gamma(1+d_1\varepsilon)}{\Gamma(1+b_1\varepsilon)} ...
\frac{\Gamma(1+d_k\varepsilon)}{\Gamma(1+b_k\varepsilon)}
\frac{\Gamma(1+d_1'\varepsilon)}{\Gamma(1+b_1'\varepsilon)} ...
\frac{\Gamma(1+d_{k'}'\varepsilon)}{\Gamma(1+b_{k'}'\varepsilon)}
\]](form_257.png)
![\[
\mbox{} (-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)}
\frac{\Gamma(i+a_2+b_2\varepsilon)}{\Gamma(i+c_2+d_2\varepsilon)} ...
\frac{\Gamma(i+a_k+b_k\varepsilon)}{\Gamma(i+c_k+d_k\varepsilon)}
S(i+o,m_1,...,m_l,x_1,...,x_l)
\]](form_324.png)
![\[
\cdot
\frac{y^{n-i}}{(n-i+c')^{m'}}
\frac{\Gamma(n-i+a_1'+b_1'\varepsilon)}{\Gamma(n-i+c_1'+d_1'\varepsilon)}
\frac{\Gamma(n-i+a_2'+b_2'\varepsilon)}{\Gamma(n-i+c_2'+d_2'\varepsilon)} ...
\frac{\Gamma(n-i+a_{k'}'+b_{k'}'\varepsilon)}{\Gamma(n-i+c_{k'}'+d_{k'}'\varepsilon)}
S(n-i+o',m_1',...,m_{l'}',x_1',...,x_{l'}')
\]](form_325.png)
Here, 

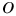
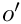
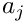
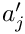
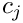
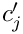

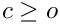

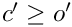
Note that the upper summation limit is 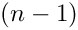
Member Function Documentation
◆ distribute_over_letter()
| ex distribute_over_letter | ( | void | ) | const |
letter is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars and basic_letters.
This routine converts the transcendental_sum_type_D to a canonical form, so that afterwards letter only contains a basic_letter.
◆ distribute_over_letter_rev()
| ex distribute_over_letter_rev | ( | void | ) | const |
letter_rev is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars and basic_letters.
This routine converts the transcendental_sum_type_D to a canonical form, so that afterwards letter_rev only contains a basic_letter.
◆ distribute_over_subsum()
| ex distribute_over_subsum | ( | void | ) | const |
subsum is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars, basic_letters, list_of_tgammas, Zsums or Ssums.
This routine converts the transcendental_sum_type_D to a canonical form, so that afterwards subsum only contains a Ssum.
The algorithm is based on the following steps:
- If an object is of type basic_letter and the difference of its index with the index member is an integer, it is combined with the letter member. Otherwise it is taken out of the sum.
- If an object is of type list_of_tgamma and the difference of its index with the index member is an integer, it is combined with the lst_of_gammas member. Otherwise it is taken out of the sum.
- If an object is of type Ssum and the difference of its index with the index member is an integer, it is stays inside the subsum. Otherwise it is taken out of the sum.
- If an object is of type Zsum and the difference of its index with the index member is an integer, it is converted to an Ssum and stays inside the subsum. Otherwise it is taken out of the sum.
◆ distribute_over_subsum_rev()
| ex distribute_over_subsum_rev | ( | void | ) | const |
subsum_rev is allowed to contain a sum of products (e.g. an expression in expanded form). Each term can contain scalars, basic_letters, list_of_tgammas, Zsums or Ssums.
This routine converts the transcendental_sum_type_D to a canonical form, so that afterwards subsum_rev only contains a Ssum.
The algorithm is based on the following steps:
- If an object is of type basic_letter and the difference of its index with
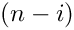
- If an object is of type list_of_tgamma and the difference of its index with
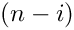
- If an object is of type Ssum and the difference of its index with
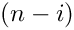
- If an object is of type Zsum and the difference of its index with
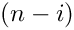
◆ eval()
|
override |
Simplifications, which are always performed are:
- If subsum is equal to 1, the subsum is replaced with S(i).
- If subsum_rev is equal to 1, the subsum_rev is replaced with S(n-i).
- If subsum is not of type Ssum, the routine distribute_over_subsum is called.
- If the difference of the upper summation index of the Ssum (in subsum) with the index member is not an integer, the Ssum is taken out of the sum. The subsum is replaced with S(i).
- If subsum_rev is not of type Ssum, the routine distribute_over_subsum_rev is called.
- If the difference of the upper summation index of the Ssum (in subsum_rev) with
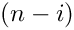
- If letter is not of type basic_letter, the routine distribute_over_letter is called.
- If the difference of the index of the basic_letter (in letter) with the index member is not zero, the index in basic_letter is adjusted.
- If letter_rev is not of type basic_letter, the routine distribute_over_letter_rev is called.
- If the difference of the index of the basic_letter (in letter_rev) with
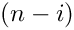
- If the difference of the index of lst_of_gammas with the index member is not zero, the index in lst_of_gammas is adjusted.
- If the difference of the index of lst_of_gammas_rev with
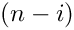
If flag_expand_status == expand_status::expansion_required, the evaluation routine performs a set of consistency checks:
- It adjusts the upper summation limit to index in subsum and to n-index in subsum_rev. If
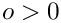

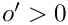

- It checks, that letter and letter_rev do not give rise to poles (e.g. that the offset

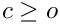

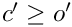
- It checks, that the
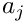
If one of the tests fails, the object is put into a zombie state.
If flag_expand_status == expand_status::check_for_poles, it assures that the Gamma functions in the numerator do not give rise to poles. The functions shift_plus_one() and shift_plus_one_rev() are used.
If flag_expand_status == expand_status::expand_gamma_functions, the Gamma functions are expanded into Euler Zagier sums. This is done by setting the expansion_required flag in the ratio_of_tgamma class.
If flag_expand_status == expand_status::do_partial_fractioning, the sum is of the form
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,m_1,...) \frac{y^{n-i}}{(n-i+c')^{m'}} S(n-i,m_1',....)
\]](form_285.png)
For 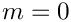
![\[
(-x)^n (-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{\left(\frac{y}{x}\right)^i}{(i+c')^{m'}} S(i,m_1',...) S(n-i,m_1,...)
\]](form_286.png)
For 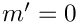
![\[
y^n (-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{\left(\frac{x}{y}\right)^i}{(i+c)^{m}} S(i,m_1,...) S(n-i,m_1',....)
\]](form_287.png)
For 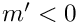
![\[
(n-i+c') = (n+c') - i
\]](form_240.png)
For 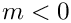
![\[
(i+c) = (n+c) - (n-i)
\]](form_242.png)
For 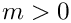
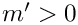
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,m_1,...) \frac{y^{n-i}}{(n-i+c')^{m'}} S(n-i,m_1',....)
\]](form_285.png)
![\[
= \frac{1}{n+c+c'} (-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^{m-1}} S(i,m_1,...) \frac{y^{n-i}}{(n-i+c')^{m'}} S(n-i,m_1',....)
\]](form_288.png)
![\[
\mbox{} +
\frac{1}{n+c+c'} (-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,m_1,...) \frac{y^{n-i}}{(n-i+c')^{m'-1}} S(n-i,m_1',....)
\]](form_289.png)
If flag_expand_status == expand_status::adjust_summation_index, we deal with sums of the form
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,m_1,...) S(n-i,m_1',....)
\]](form_290.png)
with 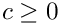
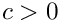
If flag_expand_status == expand_status::do_outermost_sum, the sum is of the form
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^m} S(i,m_1,...) S(n-i,m_1',....)
\]](form_291.png)
If the depth of 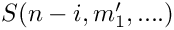
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^m} S(i,m_1,...)
=
\mbox{} - \sum\limits_{i=1}^{n}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^m} S(i,m_1,...)
+ \frac{(-x)^n}{n^m} S(n,m_1,...)
\]](form_293.png)
We now can assume that the depth of the subsum 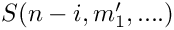
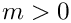
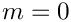
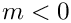
- For
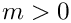
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^m} S(i,m_1,...) S(n-i,m_1',....)
\]](form_291.png)
![\[
= \sum\limits_{j=1}^n \frac{1}{j}
\left[ (-1) \sum\limits_{i=1}^{j-1}
\left( \begin{array}{c} j \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^{m-1}} S(i,m_1,...) S(j-i,m_1',....)
\right]
\]](form_294.png)
![\[
\mbox{} +
\sum\limits_{j=1}^n \frac{1}{j}
\left[ (-1) \sum\limits_{i=1}^{j-1}
\left( \begin{array}{c} j \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^{m}} S(i,m_1,...) \frac{{x_1'}^{j-i}}{(j-i)^{m_1'-1}} S(j-i,m_2',....)
\right]
\]](form_295.png)
- For
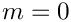
If the depth of the subsum![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
x^i S(i,m_1,...) S(n-i,m_1',....)
\]](form_296.png)
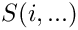
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
x^i S(n-i,m_1',....)
\]](form_297.png)
We now can assume that the depths of the subsum and subsum_rev are non-zero. We then treat the cases![\[
=
(-x)^n (-1) \sum\limits_{i=1}^{n}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\left( \frac{1}{x} \right)^i S(i,m_1',....)
+ S(n,m_1',...)
\]](form_298.png)
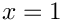
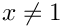
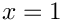
This sum can be rewritten as![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
S(i,m_1,...) S(n-i,m_1',....)
\]](form_301.png)
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
S(i,m_1,...) S(n-i,m_1',....)
\]](form_301.png)
![\[
= \frac{1}{n}
(-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x_1^i}{i^{m_1-1}} S(i,m_2,...) S(n-i,m_1',....)
\]](form_302.png)
If![\[
+ \frac{1}{n}
(-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
S(i,m_1,...) \frac{{x_1'}^{n-i}}{(n-i)^{m_1'-1}} S(n-i,m_2',....)
\]](form_303.png)
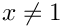
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
x^i S(i,m_1,...) S(n-i,m_1',....)
\]](form_296.png)
![\[
= (1-x)^n \sum\limits_{j=1}^n \frac{1}{j} \left( \frac{1}{1-x} \right)^j
(-1) \sum\limits_{i=1}^{j-1}
\left( \begin{array}{c} j \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{(x x_1)^i}{i^{m_1-1}} S(i,m_2,...) S(j-i,m_1',....)
\]](form_304.png)
![\[
+ (1-x)^n \sum\limits_{j=1}^n \frac{1}{j} \left( \frac{1}{1-x} \right)^j
(-1) \sum\limits_{i=1}^{j-1}
\left( \begin{array}{c} j \\ i \\ \end{array} \right)
\left( -1 \right)^i
x^i S(i,m_1,...) \frac{{x_1'}^{j-i}}{(n-i)^{m_1'-1}} S(j-i,m_2',....)
\]](form_305.png)
- For
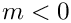
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^m} S(i,m_1,...) S(n-i,m_1',....)
\]](form_291.png)
![\[
= - n x \sum\limits_{j=0}^{-m-1}
\left( \begin{array}{c} -m-1 \\ j \\ \end{array} \right)
(-1) \sum\limits_{i=1}^{n-2}
\left( \begin{array}{c} n-1 \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^{-j}} S(i+1,m_1,...) S(n-1-i,m_1',....)
\]](form_306.png)
![\[
+ n x S(1,m_1,...) S(n-1,m_1',...)
\]](form_307.png)
◆ eval_explicit()
|
virtual |
Explicit evaluation
◆ eval_ncmul()
|
overrideprotected |
No automatic simplifications
◆ set_expansion()
| ex set_expansion | ( | void | ) | const |
Sets the flag flag_expand_status to expand_status::expansion_required. The object is then automatically expanded up to the order specified in the member variable order.
◆ shift_minus_one()
| ex shift_minus_one | ( | void | ) | const |
This routine assumes sums of the form
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,...) S(n-i,...)
\]](form_318.png)
and performs the substitution index -> index + 1.
If 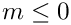
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,...) S(n-i,...)
\]](form_318.png)
![\[
=
\sum\limits_{j=0}^{-m}
\left( \begin{array}{c} -m \\ j \\ \end{array} \right)
c^{-m-j}
\mbox{} (-1) \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{i^{-j}} S(i,...) S(n-i,...)
\]](form_319.png)
If the depth of the subsum is zero, we have
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i) S(n-i,...)
\]](form_320.png)
![\[
=
\mbox{} - \frac{1}{x} \frac{1}{n+1} Z(n-2)
(-1) \sum\limits_{i=1}^{(n+1)-1}
\left( \begin{array}{c} n+1 \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c-1)^m} i S(i) S(n+1-i,...)
+ \frac{1}{c^m} S(n;m_1',...) Z(n-2)
\]](form_321.png)
If the depth of the subsum is not equal to zero, we have
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m} S(i,...) S(n-i,...)
\]](form_318.png)
![\[
=
\mbox{} - \frac{1}{x} \frac{1}{n+1} Z(n-2)
(-1) \sum\limits_{i=1}^{(n+1)-1}
\left( \begin{array}{c} n+1 \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c-1)^m} i S(i,...) S(n+1-i,...)
\]](form_322.png)
![\[
+ \frac{1}{x} \frac{1}{n+1} Z(n-2)
(-1) \sum\limits_{i=1}^{(n+1)-1}
\left( \begin{array}{c} n+1 \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c-1)^m} \frac{x_1^i}{i^{m_1-1}} S(i;m_2,...) S(n+1-i,...)
\]](form_323.png)
This routine is called from eval/adjust_summation_index only for 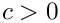
◆ shift_plus_one()
| ex shift_plus_one | ( | void | ) | const |
This routine performs the substitution index -> index - 1. The formula used is
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} ...
S(i+o,m_1,...,m_l,x_1,...,x_l)
\]](form_308.png)
![\[
\cdot
\frac{y^{n-i}}{(n-i+c')^{m'}}
\frac{\Gamma(n-i+a_1'+b_1'\varepsilon)}{\Gamma(n-i+c_1'+d_1'\varepsilon)} ...
S(n-i+o',m_1',...,m_{l'}',x_1',...,x_{l'}')
\]](form_309.png)
![\[
= (-x) n (-1)
\sum\limits_{i=1}^{n-2}
\left( \begin{array}{c} n-1 \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c+1)^m}
\frac{\Gamma(i+a_1+1+b_1\varepsilon)}{\Gamma(i+c_1+1+d_1\varepsilon)} ...
\frac{1}{i+1}
S(i+o+1,m_1,...,m_l,x_1,...,x_l)
\]](form_310.png)
![\[
\cdot
\frac{y^{n-1-i}}{(n-1-i+c')^{m'}}
\frac{\Gamma(n-1-i+a_1'+b_1'\varepsilon)}{\Gamma(n-1-i+c_1'+d_1'\varepsilon)} ...
S(n-1-i+o',m_1',...,m_{l'}',x_1',...,x_{l'}')
\]](form_311.png)
![\[
+ n \frac{x}{(c+1)^m}
\frac{\Gamma(a_1+1+b_1\varepsilon)}{\Gamma(c_1+1+d_1\varepsilon)} ...
S(o+1,m_1,...,m_l,x_1,...,x_l)
\]](form_312.png)
![\[
\cdot
\frac{y^{n-1}}{(n-1+c')^{m'}}
\frac{\Gamma(n-1+a_1'+b_1'\varepsilon)}{\Gamma(n-1+c_1'+d_1'\varepsilon)} ...
S(n-1+o',m_1',...,m_{l'}',x_1',...,x_{l'}') Z(n-2)
\]](form_313.png)
◆ shift_plus_one_rev()
| ex shift_plus_one_rev | ( | void | ) | const |
This routine takes out the term at index = n - 1. The formula used is
![\[
\mbox{} - \sum\limits_{i=1}^{n-1}
\left( \begin{array}{c} n \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} ...
S(i+o,m_1,...,m_l,x_1,...,x_l)
\]](form_308.png)
![\[
\cdot
\frac{y^{n-i}}{(n-i+c')^{m'}}
\frac{\Gamma(n-i+a_1'+b_1'\varepsilon)}{\Gamma(n-i+c_1'+d_1'\varepsilon)} ...
S(n-i+o',m_1',...,m_{l'}',x_1',...,x_{l'}')
\]](form_309.png)
![\[
= y n (-1) \sum\limits_{i=1}^{n-2}
\left( \begin{array}{c} n-1 \\ i \\ \end{array} \right)
\left( -1 \right)^i
\frac{x^i}{(i+c)^m}
\frac{\Gamma(i+a_1+b_1\varepsilon)}{\Gamma(i+c_1+d_1\varepsilon)} ...
S(i+o,m_1,...,m_l,x_1,...,x_l)
\]](form_314.png)
![\[
\cdot
\frac{y^{n-1-i}}{(n-1-i+c'+1)^{m'}}
\frac{\Gamma(n-1-i+a_1'+1+b_1'\varepsilon)}{\Gamma(n-1-i+c_1'+1+d_1'\varepsilon)} ...
\frac{1}{n-1-i+1}
S(n-1-i+o'+1,m_1',...,m_{l'}',x_1',...,x_{l'}')
\]](form_315.png)
![\[
\mbox{} - n \frac{(-x)^{n-1}}{(n-1+c)^m}
\frac{\Gamma(n-1+a_1+b_1\varepsilon)}{\Gamma(n-1+c_1+d_1\varepsilon)} ...
S(n-1+o,m_1,...,m_l,x_1,...,x_l)
\]](form_316.png)
![\[
\cdot
\frac{y}{(c'+1)^{m'}}
\frac{\Gamma(a_1'+1+b_1'\varepsilon)}{\Gamma(c_1'+1+d_1'\varepsilon)} ...
S(o'+1,m_1',...,m_{l'}',x_1',...,x_{l'}') Z(n-2)
\]](form_317.png)
The documentation for this class was generated from the following files:
Generated by